Random walk diffusion simulations in semi-permeable layered media with varying diffusivity

Abstract

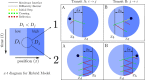
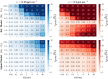
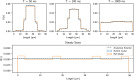
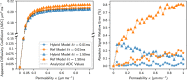
In this paper we present random walk based solutions to diffusion in semi-permeable layered media with varying diffusivity. We propose a novel transit model for solving the interaction of random walkers with a membrane. This hybrid model is based on treating the membrane permeability and the step change in diffusion coefficient as two interactions separated by an infinitesimally small layer. By conducting an extensive analytical flux analysis, the performance of our hybrid model is compared with a commonly used membrane transit model (reference model). Numerical simulations demonstrate the limitations of the reference model in dealing with step changes in diffusivity and show the capability of the hybrid model to overcome this limitation and to offer substantial gains in computational efficiency. The suitability of both random walk transit models for the application to simulations of diffusion tensor cardiovascular magnetic resonance (DT-CMR) imaging is assessed in a histology-based domain relevant to DT-CMR. In order to demonstrate the usefulness of the new hybrid model for other possible applications, we also consider a larger range of permeabilities beyond those commonly found in biological tissues.

Figure 1

(a) Left: Confocal fluorescence microscopy image of cardiomyocytes running vertically. The mean diffusion distance $\mathrm{\Delta }x\approx 30\mathrm{\mu }\text{m}$ over $100\text{ms}$ is indicated as the radius of the yellow circle. Right: Schematic of an example domain with $m=4$ compartments with indices i. Each compartment has two barriers with their corresponding locations $x_b=b_i$, $x_b=b_{i+1}=b_j$ with permeabilities ${\kappa }_i$ and ${\kappa }_j$. Note that the domain ends enforce the zero-flux boundary conditions (${\kappa }_0={\kappa }_m=0$). (b) Illustration of the behaviour of a single walker at $x_p$ performing a random step $\delta x$ towards a barrier at $x_b$. Initially, the step is divided into $\delta x_i$ and $\delta x_j$. Depending on the transit decision, the walker is either reflected elastically ($x=x_p+\delta x_i-\delta x_j$) or enters the new compartment with $D_j<D_i$. In the latter case, the remaining step after transit is modified to $\delta x_j^{\prime }$ to preserve a constant net step size. Note that $|\delta x_j^{\prime }|<|\delta x_j|$ when entering a region of lower diffusion coefficient (and conversely for $D_j<D_i$).

Figure 2

Illustration of the different possible sequences of events when a particle attempts a transit between compartments with low ($D_i$, left) and high ($D_j$, right) diffusivity. Configuration 1 places the membrane in the low diffusivity region ($x_b<x_d$), while configuration 2 places the membrane in the high diffusivity region, ($x_b>x_d$). We illustrate cases A and B, where A refers to an attempted transit from $i\to j$ and B from $j\to i$. Note that particles can freely cross the diffusivity interface $x_d$ from low (light blue) to high (dark blue) diffusivity regions, but may be reflected in attempting to cross from high to low diffusivity regions. For case 2, this results in multiple/infinite reflections in the infinitesimal gap $\delta s$ between the membrane and the diffusivity jump.

Figure 3

Histograms of walker positions after random walk simulations of the steady state. Initial positions were sampled from a uniform distribution to seed walkers with a constant density throughout the domain. We have performed the simulations with $N_p={10}^6$. We applied the reference membrane model (top) described in Eq. (5), with permeability $\kappa =0.05\mathrm{\mu }\text{m}/\text{ms}$, and the new hybrid model (bottom) from Eq. (6). Simulations were performed with varying step sizes $\delta t$ for a short and a long simulation time T. We consider $D_L=0.5\mathrm{\mu }{\text{m}}^2/\text{ms}$, $D_R=2.5\mathrm{\mu }{\text{m}}^2/\text{ms}$ and $L=20\mathrm{\mu }\text{m}$.

Figure 4

Top figures: instantaneous (numerical/analytical) and time-averaged (plotted as the average over intervals of $\mathrm{\Delta }t=20\text{ms}$) fluxes J(t) through the membrane as a function of simulation time. Bottom figure: Analytical and numerical net cumulative flux. We show results for two different step sizes $\delta t$: 20 and 0.5$\text{ms}$. Domain and simulation parameters are $D_L=0.5\mathrm{\mu }{\text{m}}^2/\text{ms}$, $D_R=2.5\mathrm{\mu }{\text{m}}^2/\text{ms}$, $\kappa =0.05\mathrm{\mu }\text{m}/\text{ms}$, $L=20\mathrm{\mu }\text{m}$, $N_p={10}^6$.

Figure 5

Global errors using the reference (upper row) and hybrid transit model (lower row) for different time steps $\delta t$, distinct diffusivity ratios $D_L:D_R$ and two different permeabilities $\kappa$. The global error measures the accuracy of the numerical simulation by calculating the area between the analytical and numerical cumulative flux during the entire simulation. Simulations were run until $t=1000\text{ms}$ with $N_p={10}^6$ walkers seeding the walkers in a partial uniform region in the left compartment $x_0\in [6,14\mathrm{\mu }\text{m}]$.

Figure 6

Illustration of the process of synthesising a 1D domain from histology data. Left figure: An example of a region of histology from a wide-field microscopy image. This is part of a large stack of histology slices obtained from the mesocardium of swine. Cardiomyocytes (red–purple) are cut perpendicular to their long axis. Extra-cellular space is white, while collagen is stained blue. Right figure: Distribution of cell sizes from automatic segmentation for the entire stack of images as well as manual labelling of a small representative region.

Figure 7

Analytical and random walk solutions using $N_p={10}^6$ walkers and a time step of $\delta t=1.5\text{ms}$. Top: Transient solution $U(x,t;x_0)$ for initial concentration at $x_0$ located in the centre of the domain considering three simulation times $50,100\text{and}1000\text{ms}$. Bottom: Steady-state solution obtained after uniformly seeding the walkers in the domain. The simulation time is set to $T=1000\text{ms}$. The reference model results in accumulation of walkers in ECS compartments. Note that this effect is visually amplified by the choice of axis data range.

Figure 8

Absolute relative signal error and ADC values for a wide range of permeability values considering a very small ($\delta t=0.01\text{ms}$) and large ($\delta t=1.5\text{ms}$) time step. All the simulations consider $N_p={10}^6$ walkers, $D_{\text{ECS}}=2\mathrm{\mu }{\text{m}}^2/\text{ms}$ and $D_{\text{ICS}}=0.5\mathrm{\mu }{\text{m}}^2/\text{ms}$.