Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Mar 9;49(9):2416-2429.
doi: 10.1080/02664763.2021.1896684. eCollection 2022.

The Log-Normal zero-inflated cure regression model for labor time in an African obstetric population

Hayala Cristina Cavenague de Souza  1 , Francisco Louzada  2 , Mauro Ribeiro de Oliveira  3 , Bukola Fawole  4 , Adesina Akintan  5 , Lawal Oyeneyin  6 , Wilfred Sanni  7 , Gleici da Silva Castro Perdoná  1
Affiliations

The Log-Normal zero-inflated cure regression model for labor time in an African obstetric population

Hayala Cristina Cavenague de Souza et al. J Appl Stat. .

Abstract

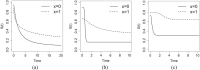
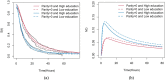
In obstetrics and gynecology, knowledge about how women's features are associated with childbirth is important. This leads to establishing guidelines and can help managers to describe the dynamics of pregnant women's hospital stays. Then, time is a variable of great importance and can be described by survival models. An issue that should be considered in the modeling is the inclusion of women for whom the duration of labor cannot be observed due to fetal death, generating a proportion of times equal to zero. Additionally, another proportion of women's time may be censored due to some intervention. The aim of this paper was to present the Log-Normal zero-inflated cure regression model and to evaluate likelihood-based parameter estimation by a simulation study. In general, the inference procedures showed a better performance for larger samples and low proportions of zero inflation and cure. To exemplify how this model can be an important tool for investigating the course of the childbirth process, we considered the Better Outcomes in Labor Difficulty project dataset and showed that parity and educational level are associated with the main outcomes. We acknowledge the World Health Organization for granting us permission to use the dataset.

Keywords: Childbirth; cure; duration of labor; survival analysis; zero-inflation.

PubMed Disclaimer

Conflict of interest statement

No potential conflict of interest was reported by the author(s).

Figures

Figure 1.
Figure 1.
Survival curves of simulation study parameter scenarios.(a) Scenario I. (b) Scenario II. (c) Scenario III.
Figure 2.
Figure 2.
Results of Log-Normal ZIC model by educational level and parity: Fitted survival curves with Kapplan Meier estimates(a) and fitted hazard function(b). (a) Survival. (b) Hazard.
Figure A1.
Figure A1.
Sample selection flow chart.
See this image and copyright information in PMC

References

    1. Barreto-Souza W., Long-term survival models with overdispersed number of competing causes, Comput. Stat. Data. Anal. 91 (2015), pp. 51–63.
    1. Beesley L.J. and Taylor J.M., Em algorithms for fitting multistate cure models, Biostatistics 20 (2019), pp. 416–432. - PMC - PubMed
    1. Berkson J. and Gage R.P., Survival curve for cancer patients following treatment, J. Am. Stat. Assoc. 47 (1952), pp. 501–515.
    1. Bertoli W., Conceição K.S., Andrade M.G., and Louzada F., A bayesian approach for some zero-modified poisson mixture models, Stat. Modelling. 20 (2020), pp. 467–501.
    1. Boag J.W., Maximum likelihood estimates of the proportion of patients cured by cancer therapy, J. R. Stat. Soc. Ser. B (Methodological) 11 (1949), pp. 15–53.