Statistical Inference with M-Estimators on Adaptively Collected Data
- PMID: 35757490
- PMCID: PMC9232184
Statistical Inference with M-Estimators on Adaptively Collected Data
Abstract
Bandit algorithms are increasingly used in real-world sequential decision-making problems. Associated with this is an increased desire to be able to use the resulting datasets to answer scientific questions like: Did one type of ad lead to more purchases? In which contexts is a mobile health intervention effective? However, classical statistical approaches fail to provide valid confidence intervals when used with data collected with bandit algorithms. Alternative methods have recently been developed for simple models (e.g., comparison of means). Yet there is a lack of general methods for conducting statistical inference using more complex models on data collected with (contextual) bandit algorithms; for example, current methods cannot be used for valid inference on parameters in a logistic regression model for a binary reward. In this work, we develop theory justifying the use of M-estimators-which includes estimators based on empirical risk minimization as well as maximum likelihood-on data collected with adaptive algorithms, including (contextual) bandit algorithms. Specifically, we show that M-estimators, modified with particular adaptive weights, can be used to construct asymptotically valid confidence regions for a variety of inferential targets.
Figures


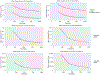
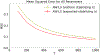

References
-
- Abbasi-Yadkori Yasin, Pál Dávid, and Szepesvári Csaba. Improved algorithms for linear stochastic bandits. In Advances in Neural Information Processing Systems, pages 2312–2320, 2011.
-
- Agrawal Shipra and Goyal Navin. Thompson sampling for contextual bandits with linear payoffs. In International Conference on Machine Learning, pages 127–135, 2013.
-
- Agresti Alan. Foundations of linear and generalized linear models. John Wiley & Sons, 2015.
-
- Bubeck Sébastien, Munos Rémi, and Stoltz Gilles. Pure exploration in multi-armed bandits problems. In International conference on Algorithmic learning theory, pages 23–37. Springer, 2009.
Grants and funding
LinkOut - more resources
Full Text Sources
