Markov chains improve the significance computation of overlapping genome annotations

Abstract

Motivation: Genome annotations are a common way to represent genomic features such as genes, regulatory elements or epigenetic modifications. The amount of overlap between two annotations is often used to ascertain if there is an underlying biological connection between them. In order to distinguish between true biological association and overlap by pure chance, a robust measure of significance is required. One common way to do this is to determine if the number of intervals in the reference annotation that intersect the query annotation is statistically significant. However, currently employed statistical frameworks are often either inefficient or inaccurate when computing P-values on the scale of the whole human genome.

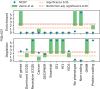
Results: We show that finding the P-values under the typically used 'gold' null hypothesis is NP-hard. This motivates us to reformulate the null hypothesis using Markov chains. To be able to measure the fidelity of our Markovian null hypothesis, we develop a fast direct sampling algorithm to estimate the P-value under the gold null hypothesis. We then present an open-source software tool MCDP that computes the P-values under the Markovian null hypothesis in O(m2+n) time and O(m) memory, where m and n are the numbers of intervals in the reference and query annotations, respectively. Notably, MCDP runtime and memory usage are independent from the genome length, allowing it to outperform previous approaches in runtime and memory usage by orders of magnitude on human genome annotations, while maintaining the same level of accuracy.

Availability and implementation: The software is available at https://github.com/fmfi-compbio/mc-overlaps. All data for reproducibility are available at https://github.com/fmfi-compbio/mc-overlaps-reproducibility.

Supplementary information: Supplementary data are available at Bioinformatics online.

Fig. 1.

An example illustrating the reduction in Theorem 1 from an instance of the multiprocessor scheduling problem to an instance of the P-value problem under ${\mathcal{H}}_0^{GS}$. The scheduling instance has $\overrightarrow{a}=\{2,2,2,2,4,7\}$, N = 6, b = 3 and w = 7. The resulting instance of the P-value problem has the length of the genome as L = 22, the reference interval set as $R=\{[6,8),[14,16)\}$, and the multiset of query interval lengths as $\mathit{lens}(Q)=\{1,1,1,1,3,6\}$. The figure shows R and an annotation $Q\prime$ with $\mathit{lens}(Q\prime )=\mathit{lens}(Q)$ and no overlap with the reference (i.e. $K(R,Q\prime )=0$). The annotation $Q\prime$ corresponds to partitioning $\overrightarrow{a}$ as $\left\{\right\{4,2\},\{7\},\{2,2,2\left\}\right\}$, which is a valid solution to the scheduling problem instance

Fig. 2.

P-values for the real datasets from Sarmashghi and Bafna (2019), shown on a negative log scale. On all datasets except EC, the sampled ${\mathcal{H}}_0^{GS}$ is not shown because every one of the 10 000 samples had less than K(R, Q) overlaps; the rule of three (Burns, 1983) implies that in this case, with 10 000 samples, the true P-value can only be said to be less than $P<3\times {10}^{-4}$ with 95% probability

Fig. 3.

Probability mass functions for the overlap statistics in the four datasets from Sarmashghi and Bafna (2019). The vertical lines show the critical values for significance level 0.05. Note that the x-axis is zoomed in around the main probability mass. The critical value is the smallest value of k for which $\text{Pr}[K(R,Q)\ge k]\le 0.05$. Supplementary Table S3 contains the raw critical values

Fig. 4.

Replication of Zarrei et al. (2015; Fig. 3b) analysis, where we use copy number losses as a reference and each of the columns as a separate query. The columns correspond to various subset of exons from RefSeq human genes; the exact descriptions are in Supplementary Table S4. The two panels show P-values for enrichment and depletion of copy number losses in the corresponding gene column. The blue dots represent the P-values produced by MCDP, the green boxes represent the P-value range reported by Zarrei et al. (2015). We clip the y-axis at the top, and the points and ranges at those boundaries actually have more extreme values. The orange dashed lines (lower) correspond to significance level 0.05, and the red dashed lines (upper) correspond to Bonferroni-adjusted significance level (i.e. $\frac{0.05}{13}$, since there are 13 experiments in this case). Note that MCDP can report the P-value for both enrichment and depletion because it computes the probability mass function for all values of K(R, Q) (A color version of this figure appears in the online version of this article)