On-demand ferrofluid droplet formation with non-linear magnetic permeability in the presence of high non-uniform magnetic fields
- PMID: 35760843
- PMCID: PMC9237107
- DOI: 10.1038/s41598-022-14624-w
On-demand ferrofluid droplet formation with non-linear magnetic permeability in the presence of high non-uniform magnetic fields
Abstract
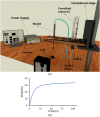
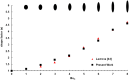
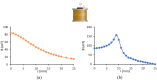
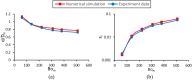
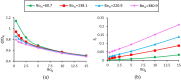
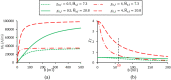
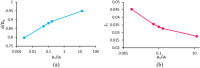
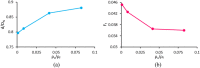
The magnetic actuation of ferrofluid droplets offers an inspiring tool in widespread engineering and biological applications. In this study, the dynamics of ferrofluid droplet generation with a Drop-on-Demand feature under a non-uniform magnetic field is investigated by multiscale numerical modeling. Langevin equation is assumed for ferrofluid magnetic susceptibility due to the strong applied magnetic field. Large and small computational domains are considered. In the larger domain, the magnetic field is obtained by solving Maxwell equations. In the smaller domain, a coupling of continuity, Navier Stokes, two-phase flow, and Maxwell equations are solved by utilizing the magnetic field achieved by the larger domain for the boundary condition. The Finite volume method and coupling of level-set and Volume of Fluid methods are used for solving equations. The droplet formation is simulated in a two-dimensional axisymmetric domain. The method of solving fluid and magnetic equations is validated using a benchmark. Then, ferrofluid droplet formation is investigated experimentally, and the numerical results showed good agreement with the experimental data. The effect of 12 dimensionless parameters, including the ratio of magnetic, gravitational, and surface tension forces, the ratio of the nozzle and magnetic coil dimensions, and ferrofluid to continuous-phase properties ratios are studied. The results showed that by increasing the magnetic Bond number, gravitational Bond number, Ohnesorge number, dimensionless saturation magnetization, initial magnetic susceptibility of ferrofluid, the generated droplet diameter reduces, whereas the formation frequency increases. The same results were observed when decreasing the ferrite core diameter to outer nozzle diameter, density, and viscosity ratios.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures








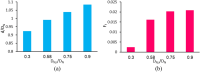



References
-
- Bijarchi MA, Favakeh A, Mohammadi K, Akbari A, Shafii MB. Ferrofluid droplet breakup process and neck evolution under steady and pulse-width modulated magnetic fields. J. Mol. Liq. 2021;343:117536.
LinkOut - more resources
Full Text Sources

