Efficient calculation of fractal properties via the Higuchi method

Abstract

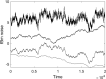
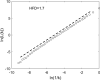
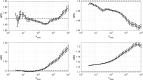
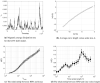
Higuchi's method of determining fractal dimension is an important, well-used, research tool that, compared to many other methods, gives rapid, efficient, and robust estimations for the range of possible fractal dimensions. One major shortcoming in applying the method is the correct choice of tuning parameter (k _max); a poor choice can generate spurious results, and there is no agreed upon methodology to solve this issue. We analyze multiple instances of synthetic fractal signals to minimize an error metric. This allows us to offer a new and general method that allows determination, a priori, of the best value for the tuning parameter, for a particular length data set. We demonstrate its use on physical data, by calculating fractal dimensions for a shell model of the nonlinear dynamics of MHD turbulence, and severe acute respiratory syndrome coronavirus 2 isolate Wuhan-Hu-1 from the family Coronaviridae.

Keywords: Brownian motion; COVID-19; Coronavirus; Fractal; Higuchi; Tuning.

Fig. 1

Examples of synthetic time series from the Davies and Harte [9] method, characterized by Hurst exponent H = 0.3, 0.5, 0.7, 0.9 (top to bottom)

Fig. 2

Average curve length versus scale size, k, for the time series with HFD = 1.7

Fig. 3

Curve showing the relationship between HFD and k_max for the FD = 1.7 time series shown in Fig. 1

Fig. 4

Curves showing the relationship between HFD and k_max for the HFD = 1.9, 1.5, 1.3, 1.1 time series shown in Fig. 1. The dashed horizontal curves show the theoretical value for the HFD

Fig. 5

Surface showing the average percentage error between the Higuchi method fractal dimension and theoretical FD = 1.7 averaged over 100 datasets of different lengths, N. The curve of least error is shown a Wavelet generation method, b Wood-Chan method, c Davies–Harte method, and d Hosking method. The curve of least error is shown as a thick grey line

Fig. 6

Comparison of the average minimum error curve (solid) and the best-fit sum of sines function (dashed)

Fig. 7

a Magnetic energy dissipation rate for the GOY shell model. b Average curve length versus scale size, k. c The relationship between HFD and kmax. d The relationship between HFD and time series length.

Fig. 8

a WH-Human-1 complete genome represented by the Peng [32] method. b Average curve length versus scale size, k