Analysis of stepped wedge cluster randomized trials in the presence of a time-varying treatment effect
- PMID: 35774016
- PMCID: PMC9481733
- DOI: 10.1002/sim.9511
Analysis of stepped wedge cluster randomized trials in the presence of a time-varying treatment effect
Abstract
Stepped wedge cluster randomized controlled trials are typically analyzed using models that assume the full effect of the treatment is achieved instantaneously. We provide an analytical framework for scenarios in which the treatment effect varies as a function of exposure time (time since the start of treatment) and define the "effect curve" as the magnitude of the treatment effect on the linear predictor scale as a function of exposure time. The "time-averaged treatment effect" (TATE) and "long-term treatment effect" (LTE) are summaries of this curve. We analytically derive the expectation of the estimator resulting from a model that assumes an immediate treatment effect and show that it can be expressed as a weighted sum of the time-specific treatment effects corresponding to the observed exposure times. Surprisingly, although the weights sum to one, some of the weights can be negative. This implies that may be severely misleading and can even converge to a value of the opposite sign of the true TATE or LTE. We describe several models, some of which make assumptions about the shape of the effect curve, that can be used to simultaneously estimate the entire effect curve, the TATE, and the LTE. We evaluate these models in a simulation study to examine the operating characteristics of the resulting estimators and apply them to two real datasets.
Keywords: cluster randomized trial; model misspecification; stepped wedge; time-varying treatment effect.
© 2022 John Wiley & Sons Ltd.
Conflict of interest statement
Conflict of interest
The authors declare no potential conflict of interests.
Figures



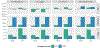


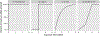
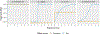
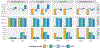
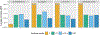

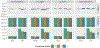

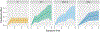


References
-
- Mdege ND, Man MS, Taylor CA, Torgerson DJ. Systematic review of stepped wedge cluster randomized trials shows that design is particularly used to evaluate interventions during routine implementation. Journal of clinical epidemiology 2011; 64(9): 936–948. - PubMed
-
- Kotz D, Spigt M, Arts IC, Crutzen R, Viechtbauer W. Use of the stepped wedge design cannot be recommended: a critical appraisal and comparison with the classic cluster randomized controlled trial design. Journal of clinical epidemiology 2012; 65(12): 1249–1252. - PubMed
-
- Mdege ND, Man MS, Taylor CA, Torgerson DJ. There are some circumstances where the stepped-wedge cluster randomized trial is preferable to the alternative: no randomized trial at all. Response to the commentary by Kotz and colleagues. Journal of clinical epidemiology 2012; 65(12): 1253. - PubMed
-
- Kotz D, Spigt M, Arts IC, Crutzen R, Viechtbauer W. Researchers should convince policy makers to perform a classic cluster randomized controlled trial instead of a stepped wedge design when an intervention is rolled out. Journal of clinical epidemiology 2012; 65(12): 1255. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
