A Multiscale Mathematical Model of Plasmodium Vivax Transmission

Abstract

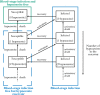
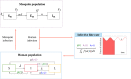
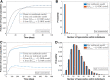
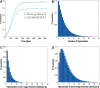
Malaria is caused by Plasmodium parasites which are transmitted to humans by the bite of an infected Anopheles mosquito. Plasmodium vivax is distinct from other malaria species in its ability to remain dormant in the liver (as hypnozoites) and activate later to cause further infections (referred to as relapses). Mathematical models to describe the transmission dynamics of P. vivax have been developed, but most of them fail to capture realistic dynamics of hypnozoites. Models that do capture the complexity tend to involve many governing equations, making them difficult to extend to incorporate other important factors for P. vivax, such as treatment status, age and pregnancy. In this paper, we have developed a multiscale model (a system of integro-differential equations) that involves a minimal set of equations at the population scale, with an embedded within-host model that can capture the dynamics of the hypnozoite reservoir. In this way, we can gain key insights into dynamics of P. vivax transmission with a minimum number of equations at the population scale, making this framework readily scalable to incorporate more complexity. We performed a sensitivity analysis of our multiscale model over key parameters and found that prevalence of P. vivax blood-stage infection increases with both bite rate and number of mosquitoes but decreases with hypnozoite death rate. Since our mathematical model captures the complex dynamics of P. vivax and the hypnozoite reservoir, it has the potential to become a key tool to inform elimination strategies for P. vivax.

Keywords: Hypnozoite activation; Hypnozoite dynamics; Multiscale model; Vivax transmission model.

Fig. 1

Overview of P. vivax disease states and complexity of the hypnozoite reservoir (adapted from White et al. (2014)). Both susceptible and infected individuals may carry hypnozoites within their liver. Activation of a hypnozoite causes a blood-stage infection, while recovery will end the blood-stage infection. The size of the hypnozoite reservoir reduces both with activation and death of a hypnozoite. Not shown explicitly in this schematic is that any individual can be bitten by an infectious mosquito, causing a blood-stage infection and possibly an increase in the size of the hypnozoite reservoir (by one or more hypnozoites). Note that blood-stage infected individuals may or may not carry hypnozoites

Fig. 2

Schematic illustration of the multiscale model. S, I and L represent the fraction of the human population that are susceptible with no hypnozoites, blood-stage infected and liver-stage infected, respectively. Individuals in the I compartment may or may not carry hypnozoites. The time-dependent parameters p(t), $k_1(t)$, and $k_T(t)$ (the probability that blood-stage infected individuals have no hypnozoites, the probability that liver-stage infected individuals have 1 hypnozoite and the expected size of the hypnozoite reservoir in liver-stage infected individuals, respectively) are derived from the within-host model and take into account the history of the force of reinfection, $\lambda (\tau ),$ where $\tau$ is the mosquito bite time and $\tau \in (0,t]$. These together make the multiscale model a system of integro-differential equations. $S_m,E_m$, and $I_m$ are the fraction of susceptible, exposed, and infectious mosquitoes, respectively. Other parameters are defined in Table 1

Fig. 3

Schematic illustration of within-host model for a single hypnozoite where H, A, C, and D represent states of establishment, activation, clearance and death of the hypnozoite, respectively. Parameters $\alpha ,\mu$ and $\gamma$ have the same meaning as in population-level model (Table 1). Figure adapted from Mehra et al. (2022) to depict the short-latency phase

Fig. 4

(A) PMF for a single hypnozoite with $(p_H(0),p_A(0),p_D(0),p_C(0))=(1,0,0,0)$ using Eqs. (7)–(10) where $p_H(t),p_A(t)$, $p_D(t),p_C(t)$ represents probability of hypnozoite establishment, activation, death, and clearance at time t, respectively. (B) Probability of no hypnozoites given blood-stage infection, p(t) using Eq. (13), probability of 1 hypnozoite given no infection, $k_1(t)$ using Eq. (17), and $k_T(t)$ using Eq. (18). Note the different scale for $k_T$. Here we have used a constant force of reinfection of $\lambda =0.005$ and other parameters are as per Table 1 (Color figure online)

Fig. 5

Comparison of results from our multiscale model with those from the $2(L_{\max }+1)$ ODE model under constant force of reinfection, $\lambda$. Subplots (A) and (C) illustrate the dynamics based on low transmission and high transmission, respectively. Subplots (B) and (D) compare the distribution of hypnozoites between our multiscale model (blue) and model containing $2(L_{\mathit{max}}+1)$ ODEs (red). In (A) and (B), transmission is low with parameters $\lambda =0.005$, $\gamma =1/10$ day${}^{-1}$, $\alpha =1/1000$ day${}^{-1}$, $\mu =1/10$ day${}^{-1}$ while in (C) and (D), transmission is high with $\lambda =0.03$ (Color figure online)

Fig. 6

Results from multiscale model for time varying force of reinfection, $\lambda (t)$. Parameters are as per Table 1. Subplot A illustrates the fraction of blood-stage (I) and liver-stage (L) infected individuals over time. Subplot B illustrates the hypnozoite distribution in population at steady state (that is, after 3500 days) obtained as per Equations (74)–(75) (without treatment) in Mehra et al. (2022). Subplot C illustrates the hypnozoite distribution within liver-stage infected (L) individuals at steady state (after 3500 days) obtained as per Equations (78)–(79) (without treatment) in Mehra et al. (2022). Finally, Subplot D illustrates the hypnozoite distribution in blood-stage infected (I) individuals at steady state (after 3500 days) obtained as per Equation (80) in Mehra et al. (2022)

Fig. 7

Sensitivity analysis showing the steady state fraction (after running numerical solution for sufficiently long) of blood-stage (I) and liver-stage (L) infected individuals when model parameters are varied for A mosquito per human, m; B average hypnozoite per bite, $\nu$; C hypnozoite activation rate, $\alpha$; and D hypnozoite death rate, $\mu$. Vertical lines indicate the parameter value used to generate the results presented in Fig. 6

Fig. 8

Schematic diagram of White et al. (2014) model, reproduced with permission. Here $S_i$ represents the fraction of the human population that are susceptible with i hypnozoites and $I_i$ represents the fraction of the human population that have a blood-stage infection with i hypnozoites. Parameters are as in Table 1

Fig. 9

Comparison of results from our multiscale model and the $2(L_{\mathit{max}}+1)$ ODE model under time varying force of reinfection, $\lambda (t)$. Subplot A shows the fractions of blood-stage and liver-stage infected individuals over time. Blood-stage and liver-stage infected individuals for the $2(L_{\mathit{max}}+1)$ ODE model is obtained by ${\sum }_{i=0}^{L_{\mathit{max}}}{I}_i$ and ${\sum }_{i=1}^{L_{\mathit{max}}}{S}_i$, respectively. Subplot B depicts the hypnozoite distribution in population at steady state (that is, after 3500 days) obtained as per Equations (74)–(75) (without treatment) in Mehra et al. (2022). Subplot C shows the Hypnozoite distribution within liver-stage infected individuals at steady state (after 3500 days) obtained as per Equations (78)–(79) (without treatment) in Mehra et al. (2022). Subplot D shows the Hypnozoite distribution in blood-stage infected (I) individuals at steady state (after 3500 days) obtained as per Equation (80) in Mehra et al. (2022). In Subplot B, C, and D, the bars are for consecutive intervals of 3 hypnozoites and the dashed lines show the whole distribution. All parameters are as per Table 1