Structure induced laminar vortices control anomalous dispersion in porous media

Abstract

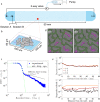
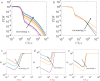
Natural porous systems, such as soil, membranes, and biological tissues comprise disordered structures characterized by dead-end pores connected to a network of percolating channels. The release and dispersion of particles, solutes, and microorganisms from such features is key for a broad range of environmental and medical applications including soil remediation, filtration and drug delivery. Yet, owing to the stagnant and opaque nature of these disordered systems, the role of microscopic structure and flow on the dispersion of particles and solutes remains poorly understood. Here, we use a microfluidic model system that features a pore structure characterized by distributed dead-ends to determine how particles are transported, retained and dispersed. We observe strong tailing of arrival time distributions at the outlet of the medium characterized by power-law decay with an exponent of 2/3. Using numerical simulations and an analytical model, we link this behavior to particles initially located within dead-end pores, and explain the tailing exponent with a hopping across and rolling along the streamlines of vortices within dead-end pores. We quantify such anomalous dispersal by a stochastic model that predicts the full evolution of arrival times. Our results demonstrate how microscopic flow structures can impact macroscopic particle transport.

Fig. 1. Characterization of the model porous structure reveals dual feature of the complex medium.

a Binary image of the disordered hyperuniform porous structure: it exhibits a complex pore network (white) interspersed among disordered grains (black) within the system. b The narrow Probability Density Function (PDF) of the pore size, exhibiting a strong peak about the average value λ_m = 27 μm. c A portion of the pore size map (λ, [μm]) highlighting the inscribed circles (cyan) along the porous network that estimate the local pore-size (see Methods a). d The dual feature of the medium characterized by the transmitting-pores (TP: green) surrounded by multiple grains and the dead-end pores (DEP: magenta) surrounded by a single grain. e Red dots represent the measured PDF of width to depth aspect ratio for DEPs, defined as the ratios between each DEP area ($\mathcal{A}$) and the mean pore-space area (${\lambda }_m^2$); the solid black line is its best fit with a Gamma distribution f_Λ.

Fig. 2. Dual geometric feature of the medium leads to two distinct regimes in the breakthrough curve of colloidal particles.

a Schematic of the experimental setup and (b) three-dimensional representation of the colloidal suspension within the porous structure. c Experimental breakthrough curve (BTC, blue dots) computed as the c(t)/c₀, where c₀ is the injected colloidal numerical density, and c(t) is the measured density eluted at time t. The dashed line represents the analytical solution of advection-dispersion equation (Eq. 26 in Supplementary Information III). The dotted line represents the prediction from diffusion based scaling (without advection). d Two snapshots of suspended (red) and deposited (green) colloids just before and 6 h after injection, respectively; TPs are represented as green areas while DEPs as magenta. e Profile of deposited (above) and suspended particles (below) along the channel length acquired at three different times (0, 1, and 6 h) after the start of the experiment.

Fig. 3. Computation of velocity field and the role of structure induced vortices on particle dispersal.

a Modulus of the Stokes flow solutions (mm/s in log-scale) in a subsection (1/5^th in length) of the porous medium used in the experiment is superposed to particles that initially occupy the TP (green) and DEP (magenta) (enlarged view in the inset). b Probability density function (PDF) of particle escape time (equivalent to the BTC) versus normalized time (t/t_PV) obtained from particle tracking in the simulated velocity field with α = 0.22 for three Péclet numbers (Pe = 68, 680, 6800). The magenta and green shades distinguish the regions of the BTC for Pe = 680 contributed by the particles shown in corresponding colors in the inset of (a). The long tail of the PDF is contributed by particles originating in the DEPs. c Fraction of particle number density re-entering a dead-end pore for the three Péclet numbers. d Qualitative identification of vortex structure inside a DEP captured by time-stacking experimental images taken at Pe ∼ 10⁵. e Close view of the vortex structures inside a DEP from the simulated velocity field. f An individual trajectory of a particle originated at the magenta dot and leaving the DEP for Pe = 6800, 680, and 68. The trajectories are color-coded with a local Péclet number Pe^* = λ_mv_p/D_m in log-scale.

Fig. 4. Conceptual model for DEP flow capturing the local particle escape time.

a A single numerically simulated trajectory (color-coded with local Péclet number Pe^* = λ_mv_p/D_m in log-scale) originating at the bottom of a 3D rectangular cavity representing a DEP (aspect ratio, Λ = 4) connected to a square channel representing a TP. A series of streamlines highlights the vortex flow structure inside the cavity. b Particles escape time probability density function (PDF, equivalent to their BTC) of a single cavity for Λ = 1, 2, 4, 8. c The same as (b) with time rescaled by diffusion time-scale ${\tau }_D={\left({\lambda }_m\mathrm{\Lambda }\right)}^2/D$.

Fig. 5. Upscale from pore-scale features to macroscopic transport.

a Schematic representation of a one-dimensional analytical model described by a straight TP connected to a collection of DEPs via Eq. (3); the distribution of DEP-size is parameterized by the PDF of aspect ratio (Λ), and their number density by the parameter α. b Comparison of the analytical prediction (solid line) from Eq. (3) of the BTC with the experimental data (dots).

Fig. 6. Parametric effects on anomalous dispersion of particles through a structurally heterogeneous porous medium.

a Particles escape time probability density function (PDF) based on numerical simulation (symbols) and the analytical model in Eq. (3) (lines) for four values of α ∈ [0.01, 0.09, 0.22, 0.5] and a Péclet number, Pe = 680. b Prediction of particle escape time PDF from the analytical model for three κ∈[−1, 0, 1] values in the DEP aspect ratios (Λ) distribution: ${\mathrm{\Lambda }}^{\kappa }{e}^{-\mathrm{\Lambda }/{\mathrm{\Lambda }}_m}$. The onset of anomalous dispersion characterized by $\mathcal{R}=F_{\mathrm{DEP}}/F\left(t\right)$ as a function of pore-volumes (t/t_PV) for (c). Pe = 6800, 680, 68 and α = 0.22. d α = 0.01, 0.09, 0.22, 0.5 and Pe = 680. e for κ = −1, 0, 1; α = 0.22, Pe = 680.