Behavioral Studies Using Large-Scale Brain Networks - Methods and Validations
- PMID: 35782044
- PMCID: PMC9244405
- DOI: 10.3389/fnhum.2022.875201
Behavioral Studies Using Large-Scale Brain Networks - Methods and Validations
Abstract
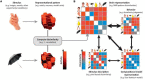
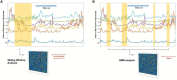
Mapping human behaviors to brain activity has become a key focus in modern cognitive neuroscience. As methods such as functional MRI (fMRI) advance cognitive scientists show an increasing interest in investigating neural activity in terms of functional connectivity and brain networks, rather than activation in a single brain region. Due to the noisy nature of neural activity, determining how behaviors are associated with specific neural signals is not well-established. Previous research has suggested graph theory techniques as a solution. Graph theory provides an opportunity to interpret human behaviors in terms of the topological organization of brain network architecture. Graph theory-based approaches, however, only scratch the surface of what neural connections relate to human behavior. Recently, the development of data-driven methods, e.g., machine learning and deep learning approaches, provide a new perspective to study the relationship between brain networks and human behaviors across the whole brain, expanding upon past literatures. In this review, we sought to revisit these data-driven approaches to facilitate our understanding of neural mechanisms and build models of human behaviors. We start with the popular graph theory approach and then discuss other data-driven approaches such as connectome-based predictive modeling, multivariate pattern analysis, network dynamic modeling, and deep learning techniques that quantify meaningful networks and connectivity related to cognition and behaviors. Importantly, for each topic, we discuss the pros and cons of the methods in addition to providing examples using our own data for each technique to describe how these methods can be applied to real-world neuroimaging data.
Keywords: data driven; graph theory; machine learning; neural network; neuroscience.
Copyright © 2022 Liu, Amey, Backer, Simon and Forbes.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures
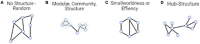




References
Publication types
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

