Optimal Sacrificial Domains in Mechanical Polyproteins: S. epidermidis Adhesins Are Tuned for Work Dissipation

Abstract

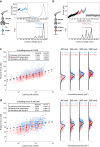
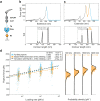
The opportunistic pathogen Staphylococcus epidermidis utilizes a multidomain surface adhesin protein to bind host components and adhere to tissues. While it is known that the interaction between the SdrG receptor and its fibrinopeptide target (FgB) is exceptionally mechanostable (∼2 nN), the influence of downstream B domains (B1 and B2) is unclear. Here, we studied the mechanical relationships between folded B domains and the SdrG receptor bound to FgB. We used protein engineering, single-molecule force spectroscopy (SMFS) with an atomic force microscope (AFM), and Monte Carlo simulations to understand how the mechanical properties of folded sacrificial domains, in general, can be optimally tuned to match the stability of a receptor-ligand complex. Analogous to macroscopic suspension systems, sacrificial shock absorber domains should neither be too weak nor too strong to optimally dissipate mechanical energy. We built artificial molecular shock absorber systems based on the nanobody (VHH) scaffold and studied the competition between domain unfolding and receptor unbinding. We quantitatively determined the optimal stability of shock absorbers that maximizes work dissipation on average for a given receptor and found that natural sacrificial domains from pathogenic S. epidermidis and Clostridium perfringens adhesins exhibit stabilities at or near this optimum within a specific range of loading rates. These findings demonstrate how tuning the stability of sacrificial domains in adhesive polyproteins can be used to maximize mechanical work dissipation and serve as an adhesion strategy by bacteria.

Figure 1

Work dissipation in adhesive polyproteins. A bacterium adheres to a substrate through an adhesion complex. A sacrificial shock dissipator domain with optimal mechanical properties buffers mechanical fluctuations and helps maintain the integrity of the surface adhesion complex under hydrodynamic forces.

Figure 2

Biasing effect and correction algorithm based on η residuals. (a) Two pathways are possible in an atomic force microscope (AFM)-SMFS assay using an RL complex to unfold an FP domain. Typical experimental data (middle) showing FP unfolding followed by complex rupture (upper trace) or complex rupture prior to FP unfolding (lower trace). (b) Biased force distributions of RL rupture (green) and FP unfolding (orange) obtained from analysis of force extension exhibiting FP unfolding. (c) True force distribution (unbiased) of the RL rupture events can be obtained by analyzing traces from both pathways. To obtain the true distribution of FP unfolding forces, a correction algorithm is required. (d) Overview of the correction algorithm to extract the true distribution of FP unfolding forces from biased experimental AFM-SMFS observations using a nonlinear least-squares fitting of η. Initial guesses for energy landscape parameters (in this case, Bell–Evans k₀ and Δx) for the FP are obtained by direct fitting of the biased experimental FP unfolding force distribution. Based on the guess, the theoretical eta value (η*) is numerically computed using eqs 4 and 5 and compared with the experimentally observed η. This process is repeated with updated energy landscape parameters for the FP domain until the tolerance on η residuals is reached.

Figure 3

Experimental validation of biasing of ddFLN4 and FIVAR unfolding forces by the VHH:mCherry complex and implementation of correction algorithm. (a, b) AFM-SMFS measurements on FIVAR domain with (a) Sdrg:Fg complex (unbiased system) and (b) VHH:mCherry complex (biased system). Experimental AFM setup, representative force trace, and the aligned contour length histogram are shown. The unfolding of FIVAR domain with an ∼31 nm increment, followed by the two-step unfolding of the ddFLN4 FP domain with ∼35 nm increments could be identified from the contour length histogram. (c) Dynamic force spectrum of FIVAR unfolding forces obtained from both (a) unbiased system using SdrG:Fg complex (blue) and (b) biased system using VHH:mCherry complex (red). (d) Dynamic force spectrum of ddFLN4 unfolding forces obtained from both (a) unbiased system using SdrG:Fg complex (blue) and (b) biased system using VHH:mCherry complex (red). The most probable rupture force and loading rates were fit using the Bell–Evans model (dashed lines). Using the fitting approach based on minimizing η residuals, we obtained new energy landscape parameters corresponding to the black dashed line. In the right-hand-side plots of (c) and (d), the black solid line represents the distribution after algorithmic correction.

Figure 4

Extracting corrected B2 unfolding parameters from biased AFM-SMFS data. (a) AFM experimental setup. (b, c) Representative force traces and the aligned contour length histograms showing the two possible dissociation pathways for the SdrG-B2 system. (d) Dynamic force spectrum of the biased B2 unfolding force (orange) and Sdrg:FgB rupture events (blue). The most probable rupture forces and loading rates were fitted using the Bell–Evans model shown in dashed lines. We used the fitting approach based on minimizing residuals of η to obtain a corrected Bell–Evans expression for the loading rate dependency of B2 domain unfolding (black dashed line) and the corresponding unfolding force distributions (right, solid black lines).

Figure 5

Monte Carlo simulations showing mechanical work (energy) dissipation as a function of the relative mechanical stability of the FP domain and the loading rate. Monte Carlo simulations under a constant loading rate were conducted on both (a) C. perfringens cohesin-dockerin RL system with variable stability of the FIVAR FP and (b) S. epidermidis SdrG:FgB RL system with variable stability of the B2 domain FP. The FP has a fixed initial off-rate k_o and the unfolding force distribution was tuned by adjusting both the energy barrier position (Δx) and the loading rate from 1 to 10¹⁰ pN/s; 5000 simulations were performed for each energy barrier position and loading rate. The simulations corresponding to the WT sacrificial (a) FIVAR and (b) B2 are shown on the plots as black dots. Two-dimensional (2D) cutouts from these three-dimensional (3D) surface plots are shown in Supporting Information Figure 5.