Contribution of Phase Resetting to Statistical Persistence in Stride Intervals: A Modeling Study

Abstract

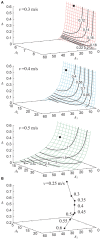
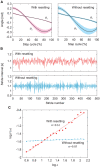
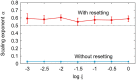
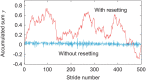
Stride intervals in human walking fluctuate from one stride to the next, exhibiting statistical persistence. This statistical property is changed by aging, neural disorders, and experimental interventions. It has been hypothesized that the central nervous system is responsible for the statistical persistence. Human walking is a complex phenomenon generated through the dynamic interactions between the central nervous system and the biomechanical system. It has also been hypothesized that the statistical persistence emerges through the dynamic interactions during walking. In particular, a previous study integrated a biomechanical model composed of seven rigid links with a central pattern generator (CPG) model, which incorporated a phase resetting mechanism as sensory feedback as well as feedforward, trajectory tracking, and intermittent feedback controllers, and suggested that phase resetting contributes to the statistical persistence in stride intervals. However, the essential mechanisms remain largely unclear due to the complexity of the neuromechanical model. In this study, we reproduced the statistical persistence in stride intervals using a simplified neuromechanical model composed of a simple compass-type biomechanical model and a simple CPG model that incorporates only phase resetting and a feedforward controller. A lack of phase resetting induced a loss of statistical persistence, as observed for aging, neural disorders, and experimental interventions. These mechanisms were clarified based on the phase response characteristics of our model. These findings provide useful insight into the mechanisms responsible for the statistical persistence of stride intervals in human walking.

Keywords: central pattern generator; human walking; neuromechanical model; phase resetting; statistical persistence; stride interval fluctuation.

Figure 1

Neuromechanical model of human walking composed of CPG model with phase resetting and compass-type biomechanical model.

Figure 2

Dependence of gait performance on parameters A₁, A₂, and Δ without noise. (A) Contour of evaluation criterion ε for parameters that generate gait speed v = 0.3, 0.4, and 0.5 m/s. Data point indicates the parameter set that minimizes ε. (B) Parameter sets that minimize ε for each gait speed v.

Figure 3

Comparison of gait fluctuations between models with and without phase resetting at gait speed v = 0.4 m/s using noise amplitude ξ = 1 (see Supplementary Movie). (A) Angles θ₁ and θ₂. Black lines and colored areas indicate the average and standard deviation, respectively. (B) Stride intervals. (C) Plot of log F(n) for log n and scaling exponent α obtained from slope of fitted line.

Figure 4

Comparison of scaling exponent α for noise amplitude ξ between models with and without phase resetting at gait speed v = 0.4 m/s. Data points and error bars correspond to the means and standard deviations, respectively, of the results of 10 simulations.

Figure 5

Comparison of stride interval fluctuations for various values of gait speed v between models with and without phase resetting using noise amplitude ξ = 10⁻². (A) Stride intervals and (B) plot of log F(n) for log n for gait speed v = 0.3, 0.4, and 0.5 m/s. (C) Scaling exponent α vs. gait speed v. Data points and error bars correspond to the means and standard deviations, respectively, of the results of 10 simulations.

Figure 6

Phase shift caused by disturbance to limit cycle of walking. After recovery, locomotion phase is shifted (x₁ + ⋯ + x_N > Nτ).

Figure 7

Comparison of accumulated sum y of stride intervals between models with and without phase resetting at gait speed v = 0.4 m/s and using noise amplitude ξ = 1 in Figure 3.