Dendritic spine morphology regulates calcium-dependent synaptic weight change

Abstract

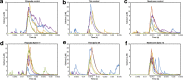
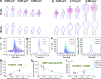
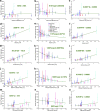
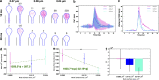
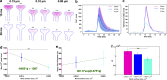
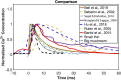
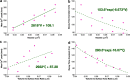
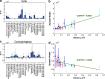
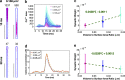
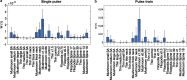
Dendritic spines act as biochemical computational units and must adapt their responses according to their activation history. Calcium influx acts as the first signaling step during postsynaptic activation and is a determinant of synaptic weight change. Dendritic spines also come in a variety of sizes and shapes. To probe the relationship between calcium dynamics and spine morphology, we used a stochastic reaction-diffusion model of calcium dynamics in idealized and realistic geometries. We show that despite the stochastic nature of the various calcium channels, receptors, and pumps, spine size and shape can modulate calcium dynamics and subsequently synaptic weight updates in a deterministic manner. Through a series of exhaustive simulations and analyses, we found that the calcium dynamics and synaptic weight change depend on the volume-to-surface area of the spine. The relationships between calcium dynamics and spine morphology identified in idealized geometries also hold in realistic geometries, suggesting that there are geometrically determined deterministic relationships that may modulate synaptic weight change.

Figure 1.

Model overview. (a) Our spatial particle–based model includes calcium influx through NMDAR and VSCC and calcium efflux to the extracellular space through PMCA and NCX pumps and to the SpApp through SERCA pumps. Arrows indicate the movement of Ca²⁺ through the labeled pump, channel, or receptor. Ω_neck represents the Dirichlet boundary condition at the base of the spine neck, at which the concentration of calcium ions is clamped to zero. Cytosolic calcium was buffered using cytosolic mobile and membrane-bound immobile calcium buffers. Inset: A change in membrane potential triggered by an EPSP and BPAP acts as the model stimulus, along with the release of glutamate molecules. (b) The geometric factors considered in our model include spine shape, spine size, neck radius and length, and SpApp size. We investigated three spine shapes: thin, mushroom-, and filopodia-shaped. (c–e) Calcium levels determine the learning rate τ_w (c) and function Ω_w (d), that in turn determine synaptic weight (e). The influence of geometry (spine volume, surface area, PSD area, etc.) and ultrastructure (SpApp, internal organelles, etc.) on calcium signaling thus has an influence on synaptic weight. θ_D and θ_P represent the thresholds for LTD and LTP, respectively. Panel a was generated using biorender.com.

Figure S1.

2-D spine profiles. (a–c) The 2-D spine profiles and the resultant rotationally symmetric spine geometries for thin spines (a), mushroom spines (b), and filopodia (c).

Figure 2.

Stochastic receptor, channel, and calcium dynamics inform deterministic synaptic weight update. (a) A realistic thin spine with a volume of 0.045 µm³ serves as an example spine to consider how stochastic receptor and channel dynamics translate into calcium transients that inform synaptic weight update. Scale bar, 0.5 μm. (b) The model stimulus includes a set voltage profile that activates both NMDARs and VSCCs. We considered a single seed run (seed 1 for the realistic thin spine 39). (c) Activated, open NMDARs over time for a single simulation in the realistic geometry shown in a. (d) Activated, open VSCCs over time for a single simulation in the realistic geometry shown in a. (e) Calcium transient due to the channel and receptor dynamics shown in c and d. (f–h) Learning rate τw (f), Ωw (g), and synaptic weight update (h) calculated from the calcium transient in e.

Figure S2.

Artificial calcium transients demonstrate how learning rate, Ωw, and synaptic weight depend on calcium temporal dynamics. (a–d) To illustrate the relationship between calcium (a), τw (b), Ωw (c), and synaptic weight (d), we constructed three artificial calcium profiles with Heaviside functions. The calcium profiles are (1) 1,000 ions for 5 ms (red line), (2) 300 ions for 5 ms (yellow dashed line), and (3) 1,000 ions for 10 ms (blue dotted line).

Figure 3.

Calcium dynamics and synaptic weight change in filopodia-shaped spines depend on spine volume-to-surface ratio. (a) Spatial plots illustrating Ca²⁺ localization at 15 and 30 ms for filopodia-shaped spines with different volumes (0.017, 0.058, and 0.138 µm³). The number above each geometry corresponds to the number of Ca²⁺ in that frame. Two random seeds are shown as examples for each geometry. Scale bars, 2 μm. (b) Mean (solid) and SD (shaded area) of Ca²⁺ transients across 50 simulations for each of the three filopodia-shaped spine sizes. (c) Variance of Ca²⁺ over time, displayed as variance divided by 1,000 ions. (d) The mean and SEM (n = 50) of the peak number of Ca²⁺ in different filopodia-shaped spine sizes shows statistically significant differences; *, P = 2.0262 × 10⁻¹¹; **, P = 9.898 × 10⁻⁸; ***, P = 4.362 10⁻²⁶ using two-tailed t-test. We fitted the trend in peak Ca²⁺ as a linear function of volume-to-surface-area ratio, ζ; r² = 0.5521 for the linear fit. (e) The decay time scales of each Ca²⁺ transient were estimated by fitting with an exponential decay function c exp(kt). The mean and SEM (n = 50) of the decay time constant, k, shows statistically significant differences across filopodia-shaped spine sizes; *, P = 1.6331 × 10⁻⁴; **, P = 0.0209; ***, P = 1.3381 × 10⁻⁶ from two-tailed t test. The mean decay time constants as a function of volume-to-surface-area ratio, ζ, were fitted with an exponential a exp(bζ); r² = 0.203 for the exponential fit. (f) The mean and SEM (n = 50) of the calculated synaptic weight change at the last time point in the simulation for all filopodia-shaped spine sizes, plotted against the volume-to-surface-area ratio, shows statistically significant differences between all cases; P₁₂ = 2.7290 × 10⁻⁵; P₂₃ = 2.8626 × 10⁻⁶; P₁₃ = 1.6321 × 10⁻¹⁴ from two-tailed t test, where 1, 2, and 3 refer to the spines in increasing size. We fitted the trend in synaptic weight as a linear function of volume-to-surface-area ratio, ζ; r² = 0.3594 for the linear fit.

Figure S3.

Trends across volume are similar to trends across volume-to-surface-area ratio. Peak calcium levels, decay time constant, and synaptic weight updates for size variations given as volumes for filopodia-shaped spines (a–c), thin spines (d–f), mushroom spines (g–i), and mushroom spines with SpApp (j–l). Peak calcium is fitted with a line with a fixed zero intercept. *, **, and *** denote statistically significant values between the different sized spines. P values for each comparison are shown in Fig. S12.

Figure S4.

Examples of calcium transients in terms of concentration for various geometries. Five examples of calcium transients in terms of concentration for the filopodia control geometry (a), thin control geometry (b), mushroom control geometry (c), realistic filopodia spine 17 (d), realistic thin spine 39 (e), and realistic mushroom spine 13 (f).

Figure 4.

Changing thin spine size modulates calcium dynamics and synaptic weight change. (a and b) Spatial plots illustrating Ca²⁺ localization at 15 and 30 ms for small thin spines with three different neck lengths, 0.07, 0.06, and 0.04 µm (a) and three different volumes, 0.035, 0.119 and 0.283 µm³ (b). The number above each geometry corresponds to the number of Ca²⁺ ions in the frame. Two random seeds are shown as examples for each geometry. Scale bars, 0.5 µm. (c) Mean (solid) and SD (shaded area) of Ca²⁺ transients across 50 simulations for each of the three thin spines with different neck lengths. (d) Variance of Ca²⁺ over time for the thin spines with different neck lengths, displayed as variance divided by 1,000 ions. (e) Mean (solid) and SD (shaded area) of Ca²⁺ transients across 50 simulations for each of the three thin spine sizes. (f) Variance of Ca²⁺ over time for the thin spines of different sizes, displayed as variance divided by 1,000 ions. (g) The mean and SEM (n = 50) of the peak number of Ca²⁺ in different thin spine sizes and with different neck lengths show an overall increasing trend. The spines of different sizes show statistically significant differences between the each size; P₁₂ = 5.2641 × 10⁻⁶; P₂₃ = 2.7377 × 10⁻⁹; P₁₃ = 5.0036 × 10^–20 from two-tailed t test, where 1, 2, and 3 denote the different sized spines in increasing size. We fitted the trend in peak Ca²⁺ as a linear function of volume-to-surface-area ratio, ζ; r² = 0.4939 for the linear fit. (h) The decay time scales of each Ca²⁺ transient were estimated by fitting with an exponential decay function c exp(kt). The mean and SEM (n = 50) of the decay time constant, k, shows statistically significant differences across thin spine sizes; P₁₂ = 4.3976 × 10⁻⁴; P₂₃ = 1.1541 × 10⁻⁴; P₁₃ = 5.4590 × 10⁻⁸ from two-tailed t test, where 1, 2, and 3 denote the different sized spines in increasing size. The mean decay time constants as a function of volume-to-surface-area ratio, ζ, were fitted with an exponential a exp(bζ); r² = 0.1630 for the exponential fit. (i) The mean and SEM (n = 50) of the calculated synaptic weight change at the last time point in the simulation for all thin spine sizes and neck lengths show an increasing trend against the volume-to-surface-area ratio. We fitted the trend in synaptic weight increase as a linear function of volume-to-surface-area ratio, ζ; r² = 0.2698 for the linear fit. The spines of different sizes show statistically significant differences between all sizes; P₁₂ = 0.0315; P₂₃ = 1.0661 × 10⁻⁵; P₁₃ = 2.5751 × 10⁻⁸ from two-tailed t test, where 1, 2, and 3 denote the different sized spines in increasing size. Inset to right of i: legend for g–i.

Figure 5.

Changing mushroom spine size modulates calcium dynamics and synaptic weight change. (a and b) Spatial plots illustrating Ca²⁺ localization at 15 and 30 ms for medium mushroom spines with three different neck lengths, 0.13, 0.10, and 0.08 µm (a) and three different volumes, 0.080, 0.271, and 0.643 µm³ (b). The number above each geometry corresponds to the number of Ca²⁺ in the frame. Two random seeds are shown as examples for each geometry. Scale bars, 0.5 µm. (c) Mean (solid) and SD (shaded area) of Ca²⁺ transients across 50 simulations for each of the three mushroom spines with different neck lengths. (d) Variance of Ca²⁺ over time for the mushroom spines with different neck length, displayed as variance divided by 1,000 ions. (e) Mean (solid) and SD (shaded area) of Ca²⁺ transients across 50 simulations for each of the three mushroom spine sizes. (f) Variance of Ca²⁺ over time for the mushroom spines of different sizes, displayed as variance divided by 1,000 ions. (g) The mean and SEM (n = 50) of the peak number of Ca²⁺ in different mushroom spine sizes and with different neck lengths show an overall increasing trend. The spines of different sizes show statistically significant differences between the each size; P₁₂ = 4.1244 × 10^–13; P₂₃ = 6.6467 × 10^–15; P₁₃ = 7.8934 × 10^–32 from two-tailed t test, where 1, 2, and 3 denote the different sized spines in increasing size. We fitted the trend in peak Ca²⁺ as a linear function of volume-to-surface-area ratio, ζ; r² = 0.5474 for the linear fit. (h) The decay time scales of each Ca²⁺ transient were estimated by fitting with an exponential decay function c exp(kt). The mean and SEM (n = 50) of the decay time constant, k, shows statistically significant differences across mushroom spine sizes; P₁₂ = 6.8175 × 10⁻⁶; P₂₃ = 6.4075 × 10⁻⁶; P₁₃ = 1.1118 × 10⁻¹⁰ from two-tailed t test, where 1, 2, and 3 denote the different sized spines in increasing size. The mean decay time constants as a function of volume-to-surface-area ratio, ζ, were fitted with an exponential a exp(bζ); r² = 0.2380 for the exponential fit. (i) The mean and SEM (n = 50) of the calculated synaptic weight change at the last time point in the simulation for all mushroom spine sizes and neck lengths show an increasing trend against the volume-to-surface-area ratio. We fitted the trend in synaptic weight increase as a linear function of volume-to-surface-area ratio, ζ; r² = 0.4224 for the linear fit. The spines of different sizes show statistically significant differences between all sizes; P₁₂ = 5.1012 × 10⁻¹⁰; P₂₃ = 2.0097 × 10⁻¹¹; P₁₃ = 2.1447 × 10⁻²³ from two-tailed t-test, where 1, 2, and 3 denote the different sized spines in increasing size. Inset to right of i: legend for g–i.

Figure 6.

Sp App size modulates synaptic weight change in mushroom spines. (a) Spatial plots at 15 and 30 ms for thin spines with SpApp of different volumes (net spine volumes of 0.026, 0.030, and 0.033 µm³). (b) Spatial plots at 15 and 30 ms for mushroom spines with SpApp of different volumes (net spine volumes of 0.203, 0.235, and 0.255 µm³). The numbers on top of the shape indicate the total number of calcium ions at that instant in both the SpApp and cytoplasm. Two random seeds are shown as examples for each geometry. Scale bars, 0.5 µm. (c and d) Calcium ions over time as mean and SD (c) and variance, displayed as variance divided by 1,000 ions (d), for all three thin spines with different SpApp sizes. Shaded regions in c denote SD. (e and f) Calcium ions over time as mean and SD (e) and variance, displayed as variance divided by 1,000 ions (f), for all three mushroom spines with different SpApp sizes. Shaded regions in e denote SD. (g) Peak calcium ion number for each thin and mushroom spine with a SpApp, with the mean and SEM (n = 50), show an increasing trend over volume-to-surface-area ratio. We fitted the trend in peak values with a linear function against the volume-to-surface-area ratio, ζ; r² = 0.6091 for the linear fit. The mushroom spines show statistically significant differences between sizes; P₁₂ = 0.0010; P₂₃ = 0.0101; P₁₃ = 4.0801 × 10⁻⁷ from two-tailed t test, where 1, 2, and 3 denote the different sized spines in increasing cytosolic volume. The thin spines show statistically significant differences only between two of the three paired cases; P₁₃ = 0.0453; P₂₃ = 0.0461 from two-tailed t test. (h) We fitted the decay dynamics of each calcium transient with (c exp[kt]) and report the decay time constant, k, as a mean and SEM (n = 50) against volume-to-surface-area ratio. The decay time constants were not statistically different for the mushroom spines, but the thin spines show a statistical difference between the second and third spine; P₂₃ = 0.0289 from two-tailed t test. We fitted the trend in decay time constants as a function of volume-to-surface-area ratio with an exponential a exp(bζ), where ζ is the volume-to-surface-area ratio; r² = 0.2219 for the fit. (i) Calculated synaptic weight change mean and SEM (n = 50) at the last time point for all three thin spines with SpApp and all three mushroom spines with SpApp show an increasing trend. We fitted the trend in synaptic weight with a linear function against the volume-to-surface-area ratio, ζ; r² = 0.2558 for the linear fit. Calculated synaptic weight change at the last time point for all three thin spines shows no statistically significant difference due to SpApp size. The mushroom spines had statistically significant differences between all cases; P₁₂ = 2.0977 × 10⁻⁴; P₂₃ = 0.0198; P₁₃ = 6.0097 × 10⁻⁷ from two-tailed t-test, where 1, 2, and 3 denote the different sized spines in increasing cytosolic volume. Inset to right of i: legend for g–i.

Figure 7.

Real spine geometries show size dependence for calcium dynamics. (a) Spines similar to the idealized geometries were selected from a reconstructed dendrite (Wu et al., 2017). Representative filopodia-shaped spines, thin spines, and mushroom spines were selected and labeled with their volume and shape. Scale bars, 0.5 μm. (b) Snapshots at 15 and 30 ms for a single seed for a filopodia-shaped spine (i), thin spine (ii), and mushroom spine (iii). (c) Calcium transients as means and SD, along with variance over time for the realistic spines of different shapes: (i and ii) filopodia-shaped spines, (iii and iv) thin spines, and (v and vi) mushroom spines. The realistic spines are labeled with their volumes.

Figure 8.

Idealized and realistic spines show overall trends in peak calcium, decay rates, and synaptic weight change with respect to various geometric parameters. We plotted all calcium peaks, decay time constants, and synaptic weight predictions for the various geometries against different geometric parameters including volume-to-PSD-area, volume, surface area, volume-to-surface-area ratio, and PSD-area-to-PM-area. We fitted the trends in peak values with a linear function against the geometric parameter. We fitted the decay dynamics of each calcium transient with c exp(kt) and report the decay time constant, k, as mean and SEM (n = 50) against the geometric parameter. We fitted the trend in synaptic weight change with a linear function against the geometric parameter. (a) All calcium peaks as mean and SEM (n = 50) across volume-to-PSD area ratio show no dependence. r² = 0.0152 for the linear fit. (b) r² = 0.0091 for the fit of decay time constants against volume-to-PSD area ratio. (c) Calculated synaptic weight change mean and SEM (n = 50) at the last time point for all idealized and realistic spines shows no dependence on volume-to-PSD area ratio. r² = 0.0060 for the linear fit. (d) All calcium peaks as mean and SEM (n = 50) across volume show a clear increasing trend. r² = 0.5666 for the linear fit. (e) r² = 0.1478 for the fit of decay time constants against volume. (f) Calculated synaptic weight change mean and SEM (n = 50) at the last time point for all idealized and realistic spines shows an increasing trend against volume. r² = 0.4635 for the linear fit. (g) All calcium peaks as mean and SEM (n = 50) across surface area show a clear increasing trend. r² = 0.5327 for the linear fit. (h) r² = 0.1427 for the fit of decay time constants against surface area. (i) Calculated synaptic weight change mean and SEM (n = 50) at the last time point for all idealized and realistic spines shows an increasing trend against surface area. r² = 0.3887 for the linear fit. (j) All calcium peaks as mean and SEM (n = 50) across volume- to- surface- area ratio show an overall increasing trend. r² = 0.351 for the linear fit. (k) r² = 0.1114 for the fit of decay time constants against volume-to-surface-area ratio. (l) Calculated synaptic weight change mean and SEM (n = 50) at the last time point for all idealized and realistic spines shows an increasing trend against volume-to-surface- area ratio. r² = 0.2815 for the linear fit. (m) All calcium peaks as mean and SEM (n = 50) across PSD surface area to PM surface area ratio show an overall increasing trend. r² = 0.1441 for the linear fit. (n) r² = 0.0428 for the fit of decay time constants against PSD-to-surface-area ratio. (o) Calculated synaptic weight change mean and SEM (n = 50) at the last time point for all idealized and realistic spines shows an increasing trend against PSD-to-surface-area ratio. r² = 0.1186 for the linear fit. Inset above e: legend for all plots.

Figure S5.

Effect of spine neck variation on synaptic plasticity in thin spines. (a) Spatial plots at 15 and 30 ms for thin spines of the same volume with different neck geometries (neck radius of 0.04, 0.06, and 0.07 μm). The number above each spine corresponds to the number of calcium ions present at that time point. Scale bar, 2 μm. (b and c) Calcium ions over time (b) and variance, displayed as variance divided by 1,000 ions (c), for all three thin spines with different neck cases. Shaded regions in b denote SD. (d) Peak calcium ion number for each thin spine with the mean and SEM (n = 50) show no statistically significant differences using a two-tailed t test. We fitted the trend in peak calcium as a linear function of spine neck base surface area; r² = 0.0009 for the linear fit. (e) We fitted the decay portion of each calcium transient with the exponential decay function c · exp(−kt). The decay time constant mean and SEM (n = 50), k, only statistically significant differences shows between the thin and thick necks; ***, P = 0.0322 from two-tailed t test. We fitted the trend in decay time constants as a function of spine neck base surface area with an exponential a · exp(−bψ), where ψ is the spine neck base surface area; r² = 0.0256 for the exponential fit. (f) Calculated synaptic weight change at the last time point for all three thin spines shows no statistically significant difference due to neck size.

Figure S6.

Effect of spine neck variation on synaptic plasticity in mushroom spines. (a) Spatial plots at 15 and 30 ms for mushroom spines of the same volume with different neck geometries (neck radius of 0.08, 0.10, and 0.13 μm). The number above each spine corresponds to the number of calcium ions present at that time point. Scale bar, 2 μm. (b and c) Calcium ions over time (b) and variance, displayed as variance divided by 1,000 ions (c), for all three mushroom spines with different neck cases. Shaded regions in b denote SD. (d) Peak calcium ion number for each mushroom spine with the mean and SEM (n = 50) show statistically significant differences between the thin and thick spines; ***, P = 0.0029 using a two-tailed t test. We fitted the trend in peak calcium as a linear function of spine neck base surface area; r² = 0.0528 for the linear fit. (e) We fitted the decay portion of each calcium transient with the exponential decay function c · exp(−kt). The decay time constant mean and SEM (n = 50), k, shows no statistically significant differences from a two-tailed t test. We fitted the trend in decay time constants as a function of spine neck base surface area with an exponential a · exp(−bψ), where ψ is the spine neck base surface area; r² = 0.0036 for the exponential fit. (f) Calculated synaptic weight change at the last time point for all three mushroom spines shows a statistically significant difference only between the thin and thick spines, ***, P = 0.0244 from two-tailed t test.

Figure S7.

Sp App size modulates synaptic weight change in thin spines. (a) Spatial plots at 15 and 30 ms for thin spines with SpApp of different volumes (spine cytosolic volumes of 0.026, 0.030, and 0.033 μm³). The numbers on top of the shape indicate the total number of calcium ions at that instant in both the SpApp and cytoplasm. (b and c) Calcium ions over time as mean and SD (b) and variance, displayed as variance divided by 1,000 ions (c), for all three thin spines with different SpApp sizes. Shaded regions in b denote SD. (d) Peak calcium ion number for each thin spine with a SpApp, with the mean and SEM (n = 50), show statistically significant differences between two of the three paired cases; *, P = 0.0461; ***, P = 0.0453 from two-tailed t test. We fitted the trend in peak values with a linear function against the cytoplasm volume; r² = 0.0145 for the linear fit. (e) We fitted the decay dynamics of each calcium transient with c · exp(−kt) and report the decay time constant, k, as a mean and SEM (n = 50). We found statistically significant differences only between the second and third spines; *, P = 0.0289 from a two-tailed t test. We fitted the trend in decay time constants as a function of cytosolic volume with an exponential a · exp(−bV), where V is the cytosolic volume; r² = 0.0177 for the fit. (f) Calculated synaptic weight change at the last time point for all three thin spines shows no statistically significant difference due to SpApp size. (g and h) We also plotted peak calcium ion number and decay time constant against the cytosolic volume-to-surface-area ratio (g and h, respectively). (g) We fitted the trend in peak values with a linear function against the volume-to-surface-area ratio; r² = 0.0214 for the linear fit. (h) We fitted the trend in decay time constants as a function of volume-to-surface-area ratio with an exponential a · exp(−bζ), where ζ is the volume-to-surface-area ratio; r² = 0.0178 for the fit.

Figure S8.

Normalized calcium transients from different experimental and computational studies. We plotted the temporal dynamics of the small idealized thin spine (0.035 µm³) and large idealized mushroom spine (0.643 µm³) versus reported experimental calcium transients from previous studies (Sabatini et al.,2002; Hoogland and Saggau, 2004; Segal and Korkotian, 2014) and computational model results from previous studies (Bell et al., 2019; Bartol et al., 2015; Rubin et al., 2005; Hu et al., 2018). The various experimental transients are reported in terms of fluorescence, and we assumed the transients were linearly proportional to concentration (Yasuda et al., 2004). We normalized the various transients and time shifted them for a more direct comparison. We plotted from Fig. 1 f in Sabatini et al. (2002), Fig. 1 in Segal and Korkotian (2014), and Fig. 2 d in Hoogland and Saggau (2004). We also compared Fig. 3 of Bell et al. (2019), Fig. 5 of Hu et al. (2018), Fig. 1 a of Rubin et al. (2005), and Fig. 7 i of Bartol et al. (2015).

Figure S9.

Previous calcium simulation results match the qualitative trends in these results. (a) We fitted the trend in peak values with a linear function against the cytoplasm volume; r² = 0.8776 for the linear fit. We fixed the y intercept at zero. (b) We fitted the decay dynamics of each calcium transient with c · exp(−kt) and report the decay time constant, k. We fitted the trend in decay time constants as a function of cytosolic volume with an exponential a · exp(−bV), where V is the cytosolic volume; r² = 0.4283 for the fit. (c) We fitted the trend in peak values with a linear function against the volume-to-surface-area ratio; r² = 0.3492 for the linear fit. (d) We fitted the trend in decay time constants as a function of volume-to-surface-area ratio with an exponential a · exp(−bζ), where ζ is the volume-to-surface-area ratio; r² = 0.9054 for the fit.

Figure S10.

Synaptic weight updates when considering Ca²⁺ in terms of ions or concentration. (a–d) Synaptic weight updates for each stochastic idealized and real geometry simulation when synaptic weight calculations are in terms of ions (a and b) and concentration (c and d). We plotted the synaptic weight changes against the spine volume for calculations using ions (b) and concentration (d). We fitted the trends using a linear function of volume; r² = 0.4635 for the ion fit and r² = 0.1229 for the concentration fit.

Figure S11.

Synaptic weight updates when considering Ca²⁺ in terms of ions or concentration for the filopodia-shaped spines. (a) Spatial plots illustrating Ca²⁺ localization at 15 and 30 ms for a filopodia-shaped spine with volume 0.138 μm³. The number above each geometry corresponds to the number of Ca²⁺ in that frame. Two random seeds are shown. Scale bars, 2 μm. (b) Mean (solid) and SD (shaded area) of Ca²⁺ transients across 50 simulations for each of the three filopodia-shaped spine sizes (0.017, 0.058, and 0.138 μm³). (c) Synaptic weight prediction for each of the filopodia geometries calculated as a function of total calcium ions. We fitted the trends using a linear function of volume-to-surface-area ratio; r² = 0.3594 for the ion fit. (d) Mean of the calcium transients for each filopodia-shaped spine size converted to concentration. (e) Synaptic weight prediction for each of the filopodia geometries calculated as a function of calcium concentration. We fitted the trends using a linear function of volume-to-surface-area ratio; r² = 0.1143 for the concentration fit. We found statistically significant differences between the first and third spines and between the second and third spines; P₁₂ = 0.1301; P₂₃ = 2.2567 × 10⁻⁴; P₁₃ = 1.1347 × 10⁻⁴ from two-tailed t test, where 1, 2, and 3 correspond to the spines in increasing volume.

Figure S12.

Two-tailed t test comparison between all simulations. We conducted two-tailed t tests between all simulations and display the h value and P value for maximum Ca²⁺ peaks (a and b), decay rate constant (c and d), and synaptic weight change (e and f). Displayed P values are truncated at two decimal points.

Figure S13.

Single pulses and multiple pulses show similar trends in synaptic weight updates across different geometries. (a) Synaptic weight change due to a single pulse of calcium for the different spine geometries. (b) Synaptic weight change due to multiple pulses of calcium for the different spine geometries.