Shape judgments in natural scenes: Convexity biases versus stereopsis

Abstract

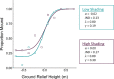
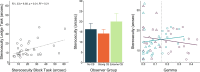
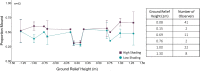
Determining the relief of upcoming terrain is critical to locomotion over rough or uneven ground. Given the significant contribution of stereopsis to perceived surface shape, it should play a crucial role in determining the shape of ground surfaces. The aim of this series of experiments was to evaluate the relative contribution of monocular and binocular depth cues to judgments of ground relief. To accomplish this goal, we simulated a depth discrimination task using naturalistic imagery. Stimuli consisted of a stereoscopically rendered grassy terrain with a central mound or a dip with varying height. We measured thresholds for discrimination of the direction of the depth offset. To determine the relationship between relief discrimination and measures of stereopsis, we used two stereoacuity tasks performed under the same viewing conditions. To assess the impact of ambiguous two-dimensional shading cues on depth judgments in our terrain task, we manipulated the intensity of the shading (low and high). Our results show that observers reliably discriminated ground reliefs as small as 20 cm at a viewing distance of 9.1 m. As the shading was intensified, a large proportion of observers (30%) exhibited a strong convexity bias, even when stereopsis indicated a concave depression. This finding suggests that there are significant individual differences in the reliance on assumptions of surface curvature that must be considered in experimental conditions. In impoverished viewing environments with limiting depth cues, these convexity biases could persist in judgments of ground relief, especially when shading cues are highly salient.

Figure 1.

An illustration of the low shading (top) and high shading (bottom) conditions. The sample images above illustrate a 0.08, 0.53, and 1.00 m mound with light from the left. These feature heights represent the low, middle, and highest ground reliefs for an observer with a moderate step size of 0.23 m.

Figure 2.

Stereopair illustrating the random dot stimuli used for the ledge task. When cross fused, the upper portion of the array will appear to be further away than the bottom portion.

Figure 3.

Illustration of the stimulus used for the bar test. When cross fused, the central white bar will appear to be further away than the outer frame.

Figure 4.

A side view illustration of the experimental layout and stimulus for the terrain task. The vertical blue line represents the projection screen, and the green line represents the ground plane of the three-dimensional imagery. The space between the projection screen (blue line) and the observer is real, while the space from the projection screen to the virtual ground plane (green line) is virtual. Observers were positioned 6.1 m from the projection screen and the ground plane of the stimulus was presented with uncrossed disparity relative to the screen plane producing the impression of the ground plane at a distance of 9.1 m. The size of the mound is not to scale.

Figure 5.

An example of one observer's psychometric function for the binocular condition in the terrain task. The plot shows the proportion of times the observer responded mound as a function of the height of the ground relief for both the low (circles) and high shading conditions (squares). The fitted values for each psychometric function are shown on the right. α represents the inflection point, JND is the difference threshold between 0.50 and 0.75 proportion correct, 1-λ represents the upper asymptote, and γ represents the lower asymptote.

Figure 6.

Average α and JND (m) for low shading (n = 39), and high shading (n = 30) conditions shown as violin plots. The white circle is the mean, the black bar is ±1 standard deviation, and the faint line is the range of the data. Each colored point represents an individuals’ data point, and the shape of the violin represents the distribution of the data. The density estimation was fit using a Gaussian kernel with a smoothing bandwidth using Silverman's rule-of-thumb (or 0.9 times the minimum standard deviation and interquartile range divided by 1.34 times the sample size to the negative one-fifth power). Thirteen participants (n = 13) were removed from the high shading condition, and four of these same participants (n = 4) were removed from the low shading condition owing to an inability to fit their psychometric functions.

Figure 7.

The average proportion mound for each group of observers, (1) No CB, (2) Strong CB, and (3) Extreme CB for the low and high shading conditions with the lighting direction from the left and right. The best fit line represents a loess fit. The shading represents the standard error of the fit. The horizontal dotted line represents the criterion for the γ value. The observers that did not achieve a fit for the psychometric functions exhibited a strong tendency to respond ‘mound’ especially in the high shading condition as shown by the U-shaped function in the bottom middle. All observers that showed a Strong CB and did not achieve a psychometric fit in the low shading condition (n = 4) also showed a Strong CB in the high shading condition.

Figure 8.

The left scatter plot shows the correlation between the stereoacuity in the ledge task and block task for each observer. The middle bar plot shows the mean stereoacuity of both stereoacuity tests for each observer group. The observer groups consisted of (1) No CB, (2) Strong CB, and (3) Extreme CB (n = 15, n = 15, and n = 13, respectively). The observer groups are split based on the high shading data where the CB was the strongest. The error bars represent one standard error of the mean. The right scatter plot shows the individual stereoacuity for the Strong CB (circles) and No CB (triangles) observers as a function of the γ value of their psychometric functions for the low (blue) and high shading condition (purple). The vertical dashed line represents the 0.15 criterion value for γ. The vertical line easily visualizes the impact of other choices of the criterion as the vertical dashed line would move to the left or right to encompass more or fewer points in each group.

Figure 9.

Average proportion response mound for the low and high shading conditions for all observers (n = 43) for the monocular test conditions. The number of observers for each ground relief is indicated in the insets and error bars indicate ±1 standard error of the mean. The number of observers varies for the different ground relief heights, because the step size was observer dependent. Error bars have not been plotted for the 0.15 and 0.76 m reliefs because only two observers were tested at these levels.

Figure 10.

The average proportion response mound for the low and high shading condition for all observers (n = 43) for the monocular test conditions. The ground relief heights are averaged for values of less than and greater than 0.38 m. The error bars represent one standard error of the mean.