Mechanistic Models of Protein Aggregation Across Length-Scales and Time-Scales: From the Test Tube to Neurodegenerative Disease

Abstract

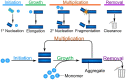
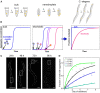
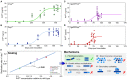
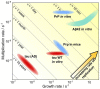
Through advances in the past decades, the central role of aberrant protein aggregation has been established in many neurodegenerative diseases. Crucially, however, the molecular mechanisms that underlie aggregate proliferation in the brains of affected individuals are still only poorly understood. Under controlled in vitro conditions, significant progress has been made in elucidating the molecular mechanisms that take place during the assembly of purified protein molecules, through advances in both experimental methods and the theories used to analyse the resulting data. The determination of the aggregation mechanism for a variety of proteins revealed the importance of intermediate oligomeric species and of the interactions with promotors and inhibitors. Such mechanistic insights, if they can be achieved in a disease-relevant system, provide invaluable information to guide the design of potential cures to these devastating disorders. However, as experimental systems approach the situation present in real disease, their complexity increases substantially. Timescales increase from hours an aggregation reaction takes in vitro, to decades over which the process takes place in disease, and length-scales increase to the dimension of a human brain. Thus, molecular level mechanistic studies, like those that successfully determined mechanisms in vitro, have only been applied in a handful of living systems to date. If their application can be extended to further systems, including patient data, they promise powerful new insights. Here we present a review of the existing strategies to gain mechanistic insights into the molecular steps driving protein aggregation and discuss the obstacles and potential paths to achieving their application in disease. First, we review the experimental approaches and analysis techniques that are used to establish the aggregation mechanisms in vitro and the insights that have been gained from them. We then discuss how these approaches must be modified and adapted to be applicable in vivo and review the existing works that have successfully applied mechanistic analysis of protein aggregation in living systems. Finally, we present a broad mechanistic classification of in vivo systems and discuss what will be required to further our understanding of aggregate formation in living systems.

Keywords: amyloid; chemical kinetics; in vivo models; mechanistic models; neurodegenerative disease; protein aggregation.

Figure 1

The different classes of processes combine into the fundamental reaction network of aggregation. Initiation is the formation of the first aggregates, without the involvement of existing aggregates. Growth is the increase in size of existing aggregates by addition of further protein subunits. Multiplication denotes any process by which existing aggregates trigger the formation of new aggregates, shown here schematically are fibril surface-catalyzed secondary nucleation and fragmentation. Finally, in vivo, aggregates can be removed by a number of clearance or degradation pathways. These fundamental classes of processes form the reaction network of aggregation, with growth and multiplication coupling together in a positive feedback loop, that gives rise to the characteristic exponential growth in aggregate mass that many systems display.

Figure 2

Complexity of reaction network can be significantly reduced by the introduction of moments. To fully describe the aggregation reaction one must account for how all the different sizes of aggregate can interact and inter-convert, leading to a highly complex reaction network with many thousands of possible species and reactions. This network can be enormously simplified by instead considering only the moments of the fibril length distribution, the aggregate number concentration, P, and the aggregate mass concentration, M. While some information about the detailed size distribution is lost in this step, the description of the system in terms of its moments is usually sufficient to fully describe most experimental data and to extract the rate constants of interest: k_n, k₂, k₋, and k+. These are the rate constants of primary nucleation, secondary nucleation, fragmentation, and elongation, respectively. Adapted from Meisl et al. (2017a).

Figure 3

Global fitting and the use of scaling to determine mechanisms. Varying a number of different experimental parameters is crucial for determining possible mechanisms. In particular, variations of the monomeric protein concentration can provide important mechanistic insights due to the differing dependence of different mechanisms on monomer concentration. A powerful and easy way to apply this technique in practice is the use of scaling exponents, which describe how a representative quantity of the aggregation reaction, such as the half time, varies with the monomer concentration. (Top) The half time can easily be extracted from kinetic traces. Plotting the half time against monomer concentration then allows the determination of the scaling exponent and exclusion of mechanisms that are inconsistent with the observed scaling. Often scaling exponents alone already allow the qualitative determination of mechanisms (here an example in which fragmentation can be excluded simply based on the scaling exponent). (Bottom) To then quantify the rates and confirm mechanisms, one performs a global fit, i.e., using one set of parameters to describe the entire dataset at all monomer concentrations, of the integrated rate laws derived for different models (points are experimental measurements of aggregate amounts, solid lines the best global fit of the model shown in the schematic, different colors denote different protein concentrations). Here the fits confirm the conclusions from the scaling analysis, that a fragmentation dominated mechanism is inconsistent with the data while a secondary nucleation dominated mechanism describe it well. Adapted from Meisl et al. (2016a, 2017b).

Figure 4

Confinement and determination of the kinetics by a stochastic nucleation event. In bulk, many initiation events take place in a short amount of time, compared to the overall timescale of the reaction (A). This leads to reproducible curves (B) and can often mean that little information about the initiation process can be obtained from an analysis of the data because they are dominated by other processes. By contrast, when the same reaction is carried out in volumes so small that initiation is rare on the timescale of the aggregation reaction, stochastic behavior emerges. Each experimental curve is governed not only by the rate constants of aggregation but also by when the random event of nucleus formation occurred. This effect can also be observed in the aggregation of polyQ in C. elegans worms (scale bars 50 μm), where each cell behaves like an independent reaction vessel (C). By globally fitting how the fraction of aggregated cells varies over time for different polyQ concentrations, the reaction order of the initiation process can be determined (D). Adapted from Sinnige et al. (2021).

Figure 5

Use of scaling analysis to determine the mechanism of replication in a living system. The concentration of prions was determined as a function of time after inoculation by prions in a number of different mouse lines, with technical and biological replicates shown as solid points (A–D). The mouse lines express the different amounts of the monomeric precursor, PrP, as shown in (E) relative to the wild type line Prnp^+/+. The rate of replication is extracted from those data by fitting of a minimal model (solid lines). In turn, the variation of the replication rate with the concentration of the precursor protein PrP allows one to determine the scaling exponent, γ = 0.6 (E). This low scaling, with the rate increasing approximately with the square root of the protein concentration, allows a range of mechanisms to be excluded and is consistent with the mechanism of prion multiplication determined for the purified protein in vitro. Adapted from Meisl et al. (2021b).

Figure 6

Quantification of timescales of aggregation across systems. A plot showing the growth rate versus the multiplication rate, for a number of proteins, using either rates determined in vivo or rates determined in vitro and extrapolated to in vivo concentrations. Along the diagonal lines, the doubling time is unchanged, thus going from the bottom left hand to the top right hand corner the rate of replication increases. Notably, the same proteins tend to aggregate orders of magnitude slower in vivo than they do in vitro, highlighting the ability of living systems to prevent aggregation. Adapted from Meisl et al. (2021a).