Modeling the impact of the vaccine on the COVID-19 epidemic transmission via fractional derivative

Abstract

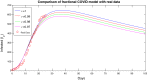
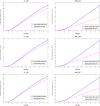
To achieve the goal of ceasing the spread of COVID-19 entirely it is essential to understand the dynamical behavior of the proliferation of the virus at an intense level. Studying this disease simply based on experimental analysis is very time consuming and expensive. Mathematical modeling might play a worthy role in this regard. By incorporating the mathematical frameworks with the available disease data it will be beneficial and economical to understand the key factors involved in the spread of COVID-19. As there are many vaccines available globally at present, henceforth, by including the effect of vaccination into the model will also support to understand the visible influence of the vaccine on the spread of COVID-19 virus. There are several ways to mathematically formulate the effect of disease on the population like deterministic modeling, stochastic modeling or fractional order modeling etc. Fractional order derivative modeling is one of the fundamental methods to understand real-world problems and evaluate accurate situations. In this article, a fractional order epidemic model $S_p{E}_p{I}_{p}E{r}_p{R}_p{D}_p{Q}_p{V}_p$ on the spread of COVID-19 is presented. $S_p{E}_p{I}_{p}E{r}_p{R}_p{D}_p{Q}_p{V}_p$ consists of eight compartments of population namely susceptible, exposed, infective, recovered, the quarantine population, recovered-exposed, and dead population. The fractional order derivative is considered in the Caputo sense. For the prophecy and tenacity of the epidemic, we compute the reproduction number $R_0$ . Using fixed point theory, the existence and uniqueness of the solutions of fractional order derivative have been studied. Furthermore, we are using the generalized Adams-Bashforth-Moulton method, to obtain the approximate solution of the fractional-order COVID-19 model. Finally, numerical results and illustrative graphic simulation are given. Our results suggest that to reduce the number of cases of COVID-19 we should reduce the contact rate of the people if the population is not fully vaccinated. However, to tackle the issue of reducing the social distancing and lock down, which have very negative impact on the economy as well as on the mental health of the people, it is much better to increase the vaccine rate and get the whole nation to be fully vaccinated.

Fig. 1

COVID model governed by Caputo fractional operator

Fig. 2

COVID model governed by Caputo fractional operator and initial condition (10999782, 200, 18, 0, 0, 0, 0)

Fig. 3

Comparison of vaccinated and non vaccinated infected population for integer-order $(\nu =1)$ and fractional-order $(\nu =0.85)$ model with vaccine rate ${\alpha }^{\nu }=000000012$ and inefficacy rate ${\sigma }^{\nu }=0.0005$ with initial condition (10999782, 200, 18, 0, 0, 0, 0, 0)

Fig. 4

Comparison of vaccinated and non vaccinated dead population for integer-order $(\nu =1)$ and fractional-order $(\nu =0.85)$ model with vaccine rate ${\alpha }^{\nu }=000000012$ and inefficacy rate ${\sigma }^{\nu }=0.0005$ with initial condition (10999782, 200, 18, 0, 0, 0, 0, 0)