Long-Term Earth-Moon Evolution With High-Level Orbit and Ocean Tide Models

Abstract

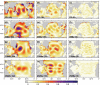
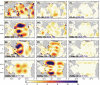
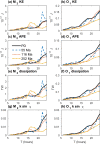
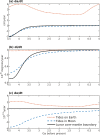
Tides and Earth-Moon system evolution are coupled over geological time. Tidal energy dissipation on Earth slows $Earth\text{'}s$ rotation rate, increases obliquity, lunar orbit semi-major axis and eccentricity, and decreases lunar inclination. Tidal and core-mantle boundary dissipation within the Moon decrease inclination, eccentricity and semi-major axis. Here we integrate the Earth-Moon system backwards for 4.5 Ga with orbital dynamics and explicit ocean tide models that are "high-level" (i.e., not idealized). To account for uncertain plate tectonic histories, we employ Monte Carlo simulations, with tidal energy dissipation rates (normalized relative to astronomical forcing parameters) randomly selected from ocean tide simulations with modern ocean basin geometry and with 55, 116, and 252 Ma reconstructed basin paleogeometries. The normalized dissipation rates depend upon basin geometry and $Earth\text{'}s$ rotation rate. Faster Earth rotation generally yields lower normalized dissipation rates. The Monte Carlo results provide a spread of possible early values for the Earth-Moon system parameters. Of consequence for ocean circulation and climate, absolute (un-normalized) ocean tidal energy dissipation rates on the early Earth may have exceeded $today\text{'}s$ rate due to a closer Moon. Prior to $\sim 3\mathrm{Ga}$ , evolution of inclination and eccentricity is dominated by tidal and core-mantle boundary dissipation within the Moon, which yield high lunar orbit inclinations in the early Earth-Moon system. A drawback for our results is that the semi-major axis does not collapse to near-zero values at 4.5 Ga, as indicated by most lunar formation models. Additional processes, missing from our current efforts, are discussed as topics for future investigation.

Keywords: Earth rotation; Earth‐Moon history; lunar orbit; ocean tides; plate tectonics.

Figure 1

(a) Ocean basin geometry at present‐day (PD). (b–d): Reconstructed basin geometries at (b) 55 Ma, (c) 116 Ma, and (d) 252 Ma.

Figure 2

Global maps of ${\mathrm{M}}_2$ amplitude (m) with present‐day (PD), 55 Ma, 116 Ma, and 252 Ma bathymetries (top to bottom rows, respectively), and $T$ values (in Equation 6) of 24, 16, and 8 hr (left, middle, and right columns, respectively).

Figure 3

As in Figure 2, but for ${\mathrm{M}}_2$ energy dissipation rate maps (mW ${\mathrm{m}}^{-2}$). Numbers given in parentheses at the bottom of each subplot present the globally integrated ${\mathrm{M}}_2$ ocean tidal dissipation rate (TW) of each simulation. Results for $T$ = 24 hr (leftmost panels) can be compared with Green et al. (2017), who found total ocean tide dissipation rates of $\left(1.44,2.12,0.90\right)$ TW for the three paleo geometries, using another ocean model with a different treatment of self‐attraction and loading and wave drag.

Figure 4

Globally integrated kinetic energy ($KE$; a and b), available potential energy ($APE$; c and d), energy dissipation rate (e and f), and $k\sin \chi$ values (g and h), for ${\mathrm{M}}_2$ (left‐hand side subplots) and ${\mathrm{O}}_1$ (right‐hand side subplots) ocean tide simulations with different values of $T$ in Equation 6, and the four bathymetries shown in Figure 1. Four additional $T$ values were used in the 55 Ma simulations, in order to better resolve the peak near 22 hr. Globally integrated $KE$ and $APE$ values are computed via Equation 13. This figure, and all subsequent figures, have legends, and the legends are not enclosed by boxes.

Figure 5

(a) Semi‐major axis $a$ and (b) inclination $i$ in simulations with constant ocean tide $k\sin \chi$ values taken from present‐day conditions. Solutions that both omit (thick blue curves) and include (thin black curves) tidal and core‐mantle boundary (CMB) dissipation within the Moon are shown. (c) Lunar equatorial tilt $I$, in the solution that includes tidal and CMB dissipation within the Moon.

Figure 6

Modeled (a) $\mathrm{E}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{h}\prime \mathrm{s}$ rotation period $2\pi /{\omega }_E$, (b) semi‐major axis $a$, and (c) Milankovitch precession period $2\pi /[d\psi /dt]$, where $d\psi /dt$, the “fundamental precession,” or “precession of the equinoxes,” is given by Equation 36 over 4.5 Ga. Four of the orbital dynamics results (see legend in (c)) are obtained with ocean tide $k\sin \chi$ values taken from simulations that assume fixed basin geometries (see Figure 1) over time. The 1,000 Monte Carlo realizations (gray curves) employ lists in which, for each value of $T$ (see Section 4), the ocean tide $k\sin \chi$ value is chosen randomly from one of the four different paleogeographies. Tidal rhythmite estimates in (a–c) are tabulated in Table 7. The black and gray filled circles in (b) represent the results of simple “constant‐Q” forward models of early Earth‐Moon system tidal evolution as calculated by Ćuk et al. (, their Table 1) with two different values (34 and 100, respectively) of the early Earth tidal quality factor $Q_E$.

Figure 7

As in Figure 6, but for (a) mean obliquity $\epsilon$ (with Milankovitch variations removed), (b) eccentricity $e$, (c) inclination $i$, and (d) lunar equatorial tilt $I$.

Figure 8

As in Figure 6, but for (a) period $2\pi /[d\overline{\omega }/dt]$ associated with the rate of change of longitude of perigee (Equation 4), (b) nodal period $-2\pi /[d\mathrm{\Omega }/dt]$ (Equation 5), (c) $\xi$, the lunar core‐mantle boundary parameter (Equation 49), and (d) $K_{Moon}/C_{Moon}$ (Equation 51), another parameter in the lunar core‐mantle boundary equations (Section 5.3). Note that $d\mathrm{\Omega }/dt$ is negative.

Figure 9

Time derivative $d/dt$ of (a) semi‐major axis $a$, (b) inclination $i$, and (c) eccentricity $e$, in the orbital dynamics simulation that employs $k\sin \chi$ values from the ocean tide model and fixed present‐day (PD) geometry. Separate time derivative terms associated with tides on Earth, tides within the Moon, and the lunar core‐mantle boundary (CMB) are shown in all three frames.

Figure 10

As in Figure 6, but for torques about the pole from tides raised on Earth. Torques from the simplified lunar torque model employed in Bartlett and Stevenson (2016), with semi‐major axis values taken from our “PD” fixed geometry simulation, are also given. Thin vertical black lines denote the approximate boundaries of the 0.6–2.6 Ga period of potential Earth rotation rate stabilization explored by Bartlett and Stevenson (2016).

Figure 11

As in Figure 6, but for $k\sin \chi$ values (a–b) and ocean tide energy dissipation rates (c–d) of (a, c) ${\mathrm{M}}_2$ and (b, d) ${\mathrm{O}}_1$.