Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Jul 18;12(1):12219.
doi: 10.1038/s41598-022-16213-3.

Fluid structure interaction study of non-Newtonian Casson fluid in a bifurcated channel having stenosis with elastic walls

Hasan Shahzad  1 , Xinhua Wang  2 , Abuzar Ghaffari  3 , Kaleem Iqbal  4 , Muhammad Bilal Hafeez  5 , Marek Krawczuk  5 , Wiktoria Wojnicz  5
Affiliations

Fluid structure interaction study of non-Newtonian Casson fluid in a bifurcated channel having stenosis with elastic walls

Hasan Shahzad et al. Sci Rep. .

Abstract

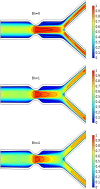
Fluid-structure interaction (FSI) gained a huge attention of scientists and researchers due to its applications in biomedical and mechanical engineering. One of the most important applications of FSI is to study the elastic wall behavior of stenotic arteries. Blood is the suspension of various cells characterized by shear thinning, yield stress, and viscoelastic qualities that can be assessed by using non-Newtonian models. In this study we explored non-Newtonian, incompressible Casson fluid flow in a bifurcated artery with a stenosis. The two-dimensional Casson model is used to study the hemodynamics of the flow. The walls of the artery are supposed to be elastic and the stenosis region is constructed in both walls. Suitable scales are used to transform the nonlinear differential equations into a dimensionless form. The problem is formulated and discretized using Arbitrary Lagrangian-Eulerian (ALE) approach. The finite element method (FEM) technique is used to solve the system of equations, together with appropriate boundary conditions. The analysis is carried out for the Bingham number, Hartmann number, and Reynolds number. The graphical results of pressure field, velocity profile, and load on the walls are assessed and used to study the influence of hemodynamic effects on stenotic arteries, bifurcation region, and elastic walls. This study shows that there is an increase in wall shear stresses (WSS) with increasing values of Bingham number and Hartmann number. Also, for different values of the Bingham number, the load on the upper wall is computed against the Hartmann number. The result indicate that load at the walls increases as the values of Bingham number and Hartmann number increase.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Figure 1
Figure 1
Problem formulation.
Figure 2
Figure 2
Comparison for the contour plots at Re=300, Anwar et al. (left) and present (right).
Figure 3
Figure 3
Velocity profile at Re = 200 for variation of Bn.
Figure 4
Figure 4
Velocity profile at Re = 400 for variation of Bn.
Figure 5
Figure 5
Velocity profile at Re = 1000 for variation of Bn.
Figure 6
Figure 6
Velocity profile at Re = 200 for variation of Ha.
Figure 7
Figure 7
Velocity profile for different Bn.
Figure 8
Figure 8
Velocity profile for different Ha.
Figure 9
Figure 9
WSS along the upper wall vs Ha for different Bn.
Figure 10
Figure 10
WSS along the upper wall vs Ha for different Re.
Figure 11
Figure 11
Upper wall’s displacement field vs Ha for different Re.
Figure 12
Figure 12
Fluid load on the upper wall vs Ha for different Bn.
See this image and copyright information in PMC

References

    1. Sankar DS. Two-phase non-linear model for blood flow in asymmetric and axisymmetric stenosed arteries. Int. J. Nonlinear Mech. 2011;46:296–305. doi: 10.1016/J.IJNONLINMEC.2010.09.011. - DOI
    1. Cokelet GR. The rheology of human blood. In: Fung YC, editor. Biomechanics. Englewood Cliffs: Prentice-Hall; 1972. pp. 63–103.
    1. Azuma T, Fukushima T. Flow patterns in stenotic blood vessel models. Biorheology. 1976;13:337–355. doi: 10.3233/BIR-1976-13602. - DOI - PubMed
    1. Young DF, Cholvin NR, Kirkeeide RL, Roth AC. Hemodynamics of arterial stenoses at elevated flow rates. Circ. Res. 1977;41:99–107. doi: 10.1161/01.RES.41.1.99. - DOI - PubMed
    1. Pontrelli G. Pulsatile blood flow in a pipe. Comput. Fluids. 1998;27:367–380. doi: 10.1016/S0045-7930(97)00041-8. - DOI