Quasi-symmetry protected topology in a semi-metal

Abstract

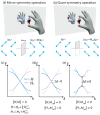
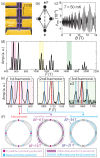
The crystal symmetry of a material dictates the type of topological band structures it may host, and therefore symmetry is the guiding principle to find topological materials. Here we introduce an alternative guiding principle, which we call 'quasi-symmetry'. This is the situation where a Hamiltonian has an exact symmetry at lower-order that is broken by higher-order perturbation terms. This enforces finite but parametrically small gaps at some low-symmetry points in momentum space. Untethered from the restraints of symmetry, quasi-symmetries eliminate the need for fine-tuning as they enforce that sources of large Berry curvature will occur at arbitrary chemical potentials. We demonstrate that a quasi-symmetry in the semi-metal CoSi stabilizes gaps below 2 meV over a large near-degenerate plane that can be measured in the quantum oscillation spectrum. The application of in-plane strain breaks the crystal symmetry and gaps the degenerate point, observable by new magnetic breakdown orbits. The quasi-symmetry, however, does not depend on spatial symmetries and hence transmission remains fully coherent. These results demonstrate a class of topological materials with increased resilience to perturbations such as strain-induced crystalline symmetry breaking, which may lead to robust topological applications as well as unexpected topology beyond the usual space group classifications.

Figure 1

(a) Illustration of a mirror symmetry operation, which acts at the whole object consistently. (b) In contrast to the mirror symmetry, quasi-symmetry operation acts differently on different parts of the system. (c) If a crystalline symmetry operation commutes with the Hamiltonian system, the band crossing point is therefore symmetry-protected. (d) In this case the Hamiltonian itself does not commute with the symmetry operation yet its first order perturbation does. This lead to the situation where though the band crossing is numerically avoided but the resulted gap size is negligible for the physical properties of the system. This type of symmetry is called quasi-symmetry. (e) If the symmetry operation does not commute with the Hamiltonian to any order of perturbation of the system, the crossing is not protected by any symmetry. This will result in a sizeable gap and lost of topological character.

Figure 2

(a) Crystal structure of CoSi. Co and Si atoms are presented as red and blue spheres respectively. (b) Ab-initio-calculated band structure of CoSi around R-point. Here 1/2 denotes orbital character while +/- stands for the spin character of the band. (c) 3D view of all Fermi surfaces, which are centered around either R- or Γ- point of the Brilloiun zone. (d) 3D view of Fermi surfaces centered around R-point with a quadrant cut. (e) Quasi-symmetry and crystalline-symmetry protected degenerate planes. (f) The Berry curvature distribution of the 1^–-band defined in (b) at different Fermi energy calculated from the model Hamiltonian Eq. (1).

Figure 3

(a) Temperature-dependent SdH oscillations with field and current applied along [100] axis. Here ρ_osc = Δρ/ρ_BG, with Δρ the oscillatory part of the magnetoresistivity, and ρ_BG the background obtained from a 3^rd-order polynomial fit to the magnetoresistivity. (b) Fast-Fourier-transformation spectrum of the SdH oscillations presented in (a) with the field window of 3 to 14 T. Two main peaks, as well as their higher-harmonic components, can be clearly observed. The suppression of peak amplitude with increasing temperature is due to the thermal damping effect. (c) Fast-fourier-transformation (FFT) spectrum of angle-dependent quantum oscillations measured at T = 2 K. Here the magnetic field is rotated within (100) plane and the angle is defined between the field direction and [001] axis. (d) Summary of angular dependence of oscillation frequencies. Here the fitting is genereated by calculating the orbital area based on band structure calculations with taking extrem magnetic breakdown due to quasi-symmetry into account (see supplement). The near-perfect fitting clearly demonstrates that quasi-symmetry is the only option to explain the experimental results of nearly angle-independent oscillation frequencies.

Figure 4

(a) Scanning electron microscope image of CoSi microdevice. A long bar roughly along [110] direction with a 2.5 by 2.4 μm² cross section is fabricated by FIB. (b) Illustration of tensile strain approximately along [110] which breaks the C₂ rotational symmetry of the crystal structure. (c) SdH oscillations with both field and current applied along the fabricated bar direction at T = 50 mK. (d) Logarithmic-scaled FFT spectrum of SdH oscillations displayed in (c). The main peaks are always accompanied with satellite peaks up to the third harmonics. (e) Enlarged view of satellite peaks correspond to the 1^st to 3^rd harmonic oscillations. The red, purple and blue vertical lines correspond to the FFT spectrum produced by the fully symmetric, crystalline-symmetry-preserved and quasi-symmetry-preserved scenarios respectively. (f) Corresponding Landau orbits for three different scenarios. Here the colored area illustrates the orbital area difference compared to the fully-symmetric case, and the black crosses represent the degeneracies that are lifted in different scenarios. Only the quasi-symmetry-preserved scenario reproduces FFT peaks that match perfectly well with the experimental data.