Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022;52(15):18226-18247.
doi: 10.1007/s10489-022-03749-0. Epub 2022 Jul 15.

Interactive group decision making method based on probabilistic hesitant Pythagorean fuzzy information representation

Gang Sun  1 , Weican Hua  2 , Guijun Wang  2
Affiliations

Interactive group decision making method based on probabilistic hesitant Pythagorean fuzzy information representation

Gang Sun et al. Appl Intell (Dordr). 2022.

Abstract

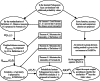
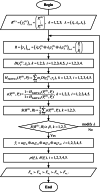
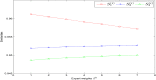
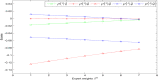
Interactive group evaluation is a decision-making method to obtain group consensus by constantly modifying the initial weight of experts. Probabilistic hesitant Pythagorean fuzzy set (PrHPFS) is to be added the corresponding probability values for each membership degree and non-membership degree on the hesitant Pythagorean fuzzy set (HPFS). It is not only a generalization of HPFS and the Pythagorean fuzzy set (PFS), but also a more comprehensive and accurate reflection of the initial decision information given by experts. Especially, it can deal with the decision-making problem of multi-attribute fuzzy information in a wider area. In this paper, some basic definitions and related operations of the probabilistic hesitant Pythagorean fuzzy numbers (PrHPFNs) are first reviewed, and propose score function and accuracy function in PrHPFNs environment. Secondly, the concepts of Hamming distance measure, weighted distance measure and degree of similarity are put forward in PrHPFNs space, and the degree of similarity of two probabilistic hesitant Pythagorean fuzzy matrices (PrHPFMs) is suggested through the aggregation operator formula of PFNs. Finally, an interactive group decision-making method is designed based on the PrHPFM and the degree of similarity under the PrHPFNs environment, the effectiveness of the method is verified by an example, so as to overcome the hesitant psychological state of experts and achieve the consistent consensus evaluation of group preference.

Keywords: Degree of similarity; Hamming distance measure; Interactive group decision making; Probabilistic hesitant Pythagorean fuzzy number (PrHPFN); Pythagorean fuzzy number (PFN).

PubMed Disclaimer

Conflict of interest statement

Conflict of interestThe authors declare that they have no conflict of interest.

Figures

Fig. 1
Fig. 1
The flow chart of the proposed group interactive decision-making method
Fig. 2
Fig. 2
The flow chart of the technical route of the proposed method
Fig. 3
Fig. 3
An intuitive flow chart of the whole decision-making process
Fig. 4
Fig. 4
Influence of adjusting expert weights to PrHPFM similarities
Fig. 5
Fig. 5
Influence of adjusting expert weights to score values
See this image and copyright information in PMC

References

    1. Atanassov KT. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20(1):87–96. doi: 10.1016/S0165-0114(86)80034-3. - DOI
    1. Yager RR (2013) Pythagorean fuzzy subsets. Proceeding Joint IFSA World Congress and NAFIPS Annual Meeting, June 24-28, 2013, Edmonton, Canada, pp: 57–61
    1. Yager RR, Abbasov AM. Pythagorean membership grades, complex numbers, and decision making. Int J Intell Syst. 2013;28(5):436–452. doi: 10.1002/int.21584. - DOI
    1. Yager RR. Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst. 2013;22(4):958–965. doi: 10.1109/TFUZZ.2013.2278989. - DOI
    1. Torra V. Hesitant fuzzy sets. Int J Intell Syst. 2010;25:529–539.

LinkOut - more resources