Pareto optimality, economy-effectiveness trade-offs and ion channel degeneracy: improving population modelling for single neurons

Abstract

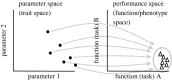
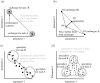
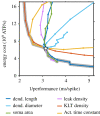
Neurons encounter unavoidable evolutionary trade-offs between multiple tasks. They must consume as little energy as possible while effectively fulfilling their functions. Cells displaying the best performance for such multi-task trade-offs are said to be Pareto optimal, with their ion channel configurations underpinning their functionality. Ion channel degeneracy, however, implies that multiple ion channel configurations can lead to functionally similar behaviour. Therefore, instead of a single model, neuroscientists often use populations of models with distinct combinations of ionic conductances. This approach is called population (database or ensemble) modelling. It remains unclear, which ion channel parameters in the vast population of functional models are more likely to be found in the brain. Here we argue that Pareto optimality can serve as a guiding principle for addressing this issue by helping to identify the subpopulations of conductance-based models that perform best for the trade-off between economy and functionality. In this way, the high-dimensional parameter space of neuronal models might be reduced to geometrically simple low-dimensional manifolds, potentially explaining experimentally observed ion channel correlations. Conversely, Pareto inference might also help deduce neuronal functions from high-dimensional Patch-seq data. In summary, Pareto optimality is a promising framework for improving population modelling of neurons and their circuits.

Keywords: Pareto front; energy efficiency; ion channel correlations; multi-objective optimization; parameter space; performance space.

Figure 1.

Degeneracy in the parameter space of biological systems (e.g. neurons with ion channels). Multiple disparate parameter configurations in the parameter (trait) space (e.g. ion conductance space) can lead to similar functional phenotypes optimized for a given task A (e.g. dendritic computation). In degenerate systems such as our brain, there is a multiple-to-one mapping between the parameter space and the phenotype space at all scales including the scale of ion channels and nerve cells (and their circuits). Each point (triangle) may represent a single neuron in a multidimensional parameter (performance) space. The schematic shows a 2D space but in real systems, parameter and performance space can have different numbers of dimensions (see also figure 8). The degeneracy and Pareto optimality concepts can be applied to any number of dimensions. For three-dimensional version of a similar schematic see, for example, fig. 4 in Mishra & Narayanan [8]. Throughout this article, we consider ‘parameter space’ and ‘trait space’ to be synonyms. Similarly, we consider ‘performance space’, ‘functional space’, ‘phenotype space’ and ‘output space’ to be synonyms. This applies also to (neuronal) ‘tasks’, ‘objectives’ and ‘functions’.

Figure 2.

Evolutionary selection based on trade-offs between multiple tasks can remove suboptimal points from (ion channel) parameter space. Each (neuronal) phenotype can be seen as a point in a two- or n-dimensional parameter space. There are two possibilities for the geometry of parameter space, as follows. (a) The (ion conductance) parameters that contribute to the function(s) of a neuron fill the entire parameter space. (b) Parameters occurring in nature (in real neurons) are restricted to a small subspace (or a curve) of the parameter space because evolution removes inefficient or ineffective parameter configurations. This can be generalized to any number of dimensions. Evolution can confine a high-dimensional parameter space to a low-dimensional manifold [37].

Figure 3.

Neuronal phenotypes that cannot be outperformed in all tasks simultaneously are Pareto optimal and lie on the Pareto front. Neuronal phenotypes, which correspond to different ion channel configurations, can be plotted in performance space based on their performance in 2 (or n) tasks. N1, N2 and N3 neurons outperform N4 and N6 in at least one task. Best phenotypes for a given task (A or B) are referred to as archetypes (A or B, respectively). Pareto optimal neurons that are close to archetypes are called task specialists. Neurons that are in the middle can be called generalists. Based on Alon [39]. See also Pallasdies et al. [34].

Figure 4.

Evolutionary trade-offs between different tasks reduce the performance space to a Pareto front. The key hypothesis is that evolutionary selection based on multi-task trade-offs removed suboptimal neuronal phenotypes from performance space and greatly simplified performance (and the corresponding parameter) space. Based on Alon [39]. Caveat: if measured neuronal phenotypes do not lie on a Pareto front predicted by a Pareto analysis, this could mean that the analysis neglected some important tasks or that neurons are not Pareto optimal for the studied tasks (see [34]).

Figure 5.

Trade-offs between 2 or 3 tasks reduce parameter space to low-dimensional Pareto fronts in the form of a line or a triangle, respectively. (a) Archetypes are located at peaks of a task performance. Contours indicate a monotonic drop in performance for locations further away from archetypes. (b) Nonoptimal neurons (N4) are more distant from archetypes than neurons on the Pareto front (N1,2,3), which is the line between archetypes (N1,2). (c,d) Hypothetical neurons that are concurrently optimized for 2 or 3 objectives (e.g. dendritic computation, its energy efficiency and robustness) would be found on a line segment or inside a triangle with specialists near the 2 or 3 vertices (archetypes), respectively. Based on Alon [39].

Figure 6.

Simulated neurons in the medial superior olive (MSO) are Pareto optimal for a 2-task trade-off between functional effectiveness and energy efficiency (economy). The figure shows a performance space for 2 tasks simulated in MSO neuron models. Simulations were run in conductance-based neuronal models with simplified morphologies. Performance in dendritic computation (task A, x-axis) in the form of temporal coincidence detection for inputs (underlying sound localization in the MSO) is plotted against performance with respect to energy efficiency (task B, y-axis). The grey line indicates the Pareto front with models that are optimal for the trade-off between the 2 tasks. Coloured curves show models with varied morphological and biophysical (ion channel) parameters. Energy cost was estimated using a standard approach for converting ionic currents into ATP. KLT: low threshold potassium current. Note that a model, which was well constrained by experimental data (open star), is close to the Pareto front and displays strong performance in coincidence detection and high energy efficiency (i.e. low energy cost). Reproduced from Remme et al. [65], licensed under Creative Commons Attribution License. https://doi.org/10.1371/journal.pcbi.1006612.g004.

Figure 7.

L5 pyramidal tract neurons (L5 PCs) might be Pareto optimal for a 2-task trade-off between dendritic computation and energy efficiency. Inspired by population modelling of L5 PCs by Bast & Oberlaender [91], we hypothesize that Pareto optimal parameter space (i.e. the Pareto front) for K⁺ and Ca²⁺ channels (referring mainly to fast noninactivating potassium channel Kv3.1 and high-/low-voltage activated calcium channels) might be a line. L5 PC models with low Kv3.1 and Ca²⁺ channel expression (in the dendritic hot zone) compromise optimally between dendritic computation (i.e. dendritic spikes and BAC firing) and low energy costs [91]. Grey line: a hypothetical Pareto front with models jointly optimal for combined 2 tasks (filled circles). Grey arrow: a hypothetical model with a relatively low (experimentally observed) expression of Kv3.1 is close to the Pareto front and displays a good combined performance in energy efficiency (archetype 1) and dendritic computation (archetype 2). Open circles: Pareto non-optimal models. See text for more details.

Figure 8.

Pareto task inference (ParTI) may help infer main functions of neurons from single-cell ion channel expression data. High-dimensional datasets, e.g. ion channel expression data from Patch-seq experiments, can be reduced to a 3-dimensional parameter space by principal component analysis (PCA). According to Pareto theory, trade-offs between n tasks will lead to data points filling out geometrical objects (Pareto fronts) with a shape of polytopes with n vertices (2 in A, 3 in B, 4 in C). The vertices (sharp corners) in measured datasets could be used to infer the key tasks of given neuron types as shown previously for nonneuronal cell types (e.g. liver cells—see [100]). However, future research is needed to clarify whether doing PCA first would give the most significant functional archetypes or would lead to a loss in archetypes by projecting to a lower-dimensional space. The figure is based on Alon [39].