Quantifying the hydrodynamic contribution to electrical transport in non-Brownian suspensions

Abstract

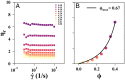
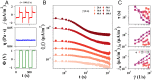
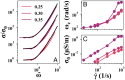
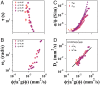
Electrical transport in semiconducting and metallic particle suspensions is an enabling feature of emerging grid-scale battery technologies. Although the physics of the transport process plays a key role in these technologies, no universal framework has yet emerged. Here, we examine the important contribution of shear flow to the electrical transport of non-Brownian suspensions. We find that these suspensions exhibit a strong dependence of the transport rate on the particle volume fraction and applied shear rate, which enables the conductivity to be dynamically changed by over 10⁷ decades based on the applied shear rate. We combine experiments and simulations to conclude that the transport process relies on a combination of charge and particle diffusion with a rate that can be predicted using a quantitative physical model that incorporates the self-diffusion of the particles.

Keywords: Stokesian dynamics; charge carrier diffusion; electrical properties; rheology; suspensions.

Fig. 1.

(A and B) Reduced viscosity ${\eta }_r$ versus $\dot{\gamma }$ as a function of $\varphi$ (0 to 0.40) (A) and the averaged reduced viscosity ${\eta }_r$ versus $\varphi$, solid line: fit to the modified Kreiger-Dougherty equation (B).

Fig. 2.

(A and B) Transient current density $j$ (Top), reduced viscosity ${\eta }_r$ (Middle), and $\dot{\gamma }$ (Bottom) versus time subjected to (A) a sequence of step-up and step-down shear rate tests with a 30-s hold at 0 1/s (ϕ = 0.35) and (B) flow reversal tests where the flow is initiated in the forward direction at 100 1/s for 30 s and then instantaneously reversed for 30 s at the same shear rate in the opposite direction before returning to the 0 1/s for 30 s. (C) The steady-state current density $j_{ss}$ versus shear rate for each volume fraction tested. Note measurements below the resolution of the source meter are not shown. The inset shows that the electric field is applied along the flow gradient direction for parallel plate geometry separated by gap $h$.

Fig. 3.

Chronoamperometry of a $\varphi = 0.30$ suspension. (A) Transient current density $j$ (Top), viscosity $\eta$ (Middle), and potential $\mathrm{\Phi }$ (Bottom) for a $\dot{\mathrm{\gamma }}=100 1/s$. (B) Mean transient current averaged over six pulses as a function of shear rate (specified in the legend). (C) Results of fitting of average current relaxation curve to [4], including the measured relaxation rate τ (Top), the initial current density (Middle), and the steady-state current density (Bottom) for each volume fraction (0.20, 0.25, 0.30, 0.35).

Fig. 4.

(A) The normalized conductivity $\mathrm{\sigma }/{\mathrm{\sigma }}_0$ plotted versus the dimensionless frequency $\omega /f_e$ as a function of shear rate and volume fraction in Couette dielectric geometry. For each volume fraction, the curves are offset by a multiplicative factor of 5. (B) ${\mathrm{\omega }}_c$ and (C) ${\mathrm{\sigma }}_0$ versus $\dot{\mathrm{\gamma }}$ for each volume fraction determined from fits to [6].

Fig. 5.

(A–D) Summary of the electrical measurements versus the scaling parameter $\varphi \dot{\gamma }{a}^{2}g\left(\varphi \right)$ for $\varphi$ (0.25, 0.30, 0.35, 0.40), (A) current relaxation time $\mathrm{\tau }$, (B) microscopic transport rate ${\mathrm{\omega }}_c$, (C) specific conductivity $\mathrm{\sigma }/\varphi$ calculated from the DC measurements for $\varphi$ (0.25, 0.30, 0.35, 0.40) and AC measurements for $\varphi$, and (D) $D_c$ calculated using $a^2{\mathrm{\omega }}_c$ and $h^2/4\tau$ for all volume fractions and shear rates. The black solid line is $0.5\varphi \dot{\gamma }{a}^{2}g\left(\varphi \right)$. The colors of the symbols correspond with the volume fraction.

Fig. 6.

(A) Comparison of the measured, simulated, and predicted gradient diffusivities ${\tilde{D}}_i^y$ for the particles (i = p) and the charges (i = c). (B and C) The PDF of a displacement of magnitude $\mathrm{\Delta }\tilde{y}$ for the (B) particles and (C) charges for $\varphi$ (0.25, 0.30, 0.35). (D) PDF of cluster size in gradient direction ${\text{y}}_{\text{c}}$.