Haisu: Hierarchically supervised nonlinear dimensionality reduction

Abstract

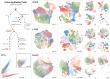
We propose a novel strategy for incorporating hierarchical supervised label information into nonlinear dimensionality reduction techniques. Specifically, we extend t-SNE, UMAP, and PHATE to include known or predicted class labels and demonstrate the efficacy of our approach on multiple single-cell RNA sequencing datasets. Our approach, "Haisu," is applicable across domains and methods of nonlinear dimensionality reduction. In general, the mathematical effect of Haisu can be summarized as a variable perturbation of the high dimensional space in which the original data is observed. We thereby preserve the core characteristics of the visualization method and only change the manifold to respect known or assumed class labels when provided. Our strategy is designed to aid in the discovery and understanding of underlying patterns in a dataset that is heavily influenced by parent-child relationships. We show that using our approach can also help in semi-supervised settings where labels are known for only some datapoints (for instance when only a fraction of the cells are labeled). In summary, Haisu extends existing popular visualization methods to enable a user to incorporate labels known a priori into a visualization, including their hierarchical relationships as defined by a user input graph.

Fig 1. Users can control the effect of an input hierarchy on the resulting embedding.

We demonstrate the effect of Haisu as applied to t-SNE, UMAP, and PHATE with an input graph on a set of random points. In (A) we display the unmodified embedding of each NLDR method without HAISU or any hierarchical prior. In (B), we demonstrate the default mode of Haisu where self-distance = 0; at higher str values this results in a stronger hierarchical effect on the original embedding. In (C) self-distance = 1 for the disconnected class (blue), which is penalized for clustering near itself and spreads back toward classes each point is most similar to. In (D) self-distance = 0.5 which still applies the hierarchy but encourages more inter-class interaction than (B). Finally, in (E) self-distance = 1 for all classes, which penalizes intra-class clustering, resulting in a much looser representation of the hierarchy compared with (B).

Fig 2. For this dataset, Haisu applies an input hierarchy based on cell function and lineage to guide the identification of sub-clusters.

We display the effect of our method on popular nonlinear DR approaches and PCA at multiple ‘strength’ values (str), a tunable factor between 0 and (up to) 1 to control the strength of our hierarchical distancing function. Compared to raw NLDR (str = 0), Haisu reveals sub-clusters of T cells and better expresses the subtle relationship between datapoints in each method.

Fig 3. Haisu applied to anatomical embryonic cardiac cell subpopulations via a proximity-based hierarchy.

The raw embeddings of each method indicate two primary clusters with cell label assignments that are spaced out within each cluster. Haisu helps to add clarity to the embedding in a manner true to the known external hierarchy. Labels are assumed to be 100% accurate as they are location-based, but anatomic regions can have similar transcriptomic profiles. Thus, Haisu in this context, factors in gene expression and location when determining a lower dimensional embedding at an appropriate strength.

Fig 4. We illustrate the effect of Haisu within the context of an epithelial differentiation hierarchy in the context of healthy and ulcerative colitis patients.

In this dataset, strength factors up to 0.8 uphold appearance of the raw embedding. Thus, with sufficient confidence in cell type labels, Haisu preserves the structure of the NLDR method while also allowing a simpler examination of more subtle inter-cluster relationships.

Fig 5. Haisu does not compromise the embedding of cells that do not have a label in the input graph.

We depict 0% and 100% replacement of the TA-1 label with a ‘dummy’ label that is not present in the hierarchy across t-SNE, UMAP, and PHATE. Even at high strength values (str) of the hierarchical distancing factor, Haisu maintains relationships in the embedding circled in the figure. Notably, TA 1 cells remain close to Cycling TA cells across the embeddings at 100% removal despite their distance in the hierarchy graph. Thus, we do not comprise the integrity of each NLDR method, allowing for the observation of unknown classes in the context of a strongly influential, known hierarchy.