Asymmetric and adaptive reward coding via normalized reinforcement learning
- PMID: 35862443
- PMCID: PMC9345478
- DOI: 10.1371/journal.pcbi.1010350
Asymmetric and adaptive reward coding via normalized reinforcement learning
Abstract
Learning is widely modeled in psychology, neuroscience, and computer science by prediction error-guided reinforcement learning (RL) algorithms. While standard RL assumes linear reward functions, reward-related neural activity is a saturating, nonlinear function of reward; however, the computational and behavioral implications of nonlinear RL are unknown. Here, we show that nonlinear RL incorporating the canonical divisive normalization computation introduces an intrinsic and tunable asymmetry in prediction error coding. At the behavioral level, this asymmetry explains empirical variability in risk preferences typically attributed to asymmetric learning rates. At the neural level, diversity in asymmetries provides a computational mechanism for recently proposed theories of distributional RL, allowing the brain to learn the full probability distribution of future rewards. This behavioral and computational flexibility argues for an incorporation of biologically valid value functions in computational models of learning and decision-making.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


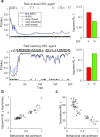
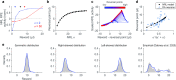
Similar articles
-
Nutrient-Sensitive Reinforcement Learning in Monkeys.J Neurosci. 2023 Mar 8;43(10):1714-1730. doi: 10.1523/JNEUROSCI.0752-22.2022. Epub 2023 Jan 20. J Neurosci. 2023. PMID: 36669886 Free PMC article.
-
Neuro-Inspired Reinforcement Learning to Improve Trajectory Prediction in Reward-Guided Behavior.Int J Neural Syst. 2022 Sep;32(9):2250038. doi: 10.1142/S0129065722500381. Epub 2022 Aug 19. Int J Neural Syst. 2022. PMID: 35989578
-
Reinforcement learning and its connections with neuroscience and psychology.Neural Netw. 2022 Jan;145:271-287. doi: 10.1016/j.neunet.2021.10.003. Epub 2021 Oct 22. Neural Netw. 2022. PMID: 34781215
-
Distributional Reinforcement Learning in the Brain.Trends Neurosci. 2020 Dec;43(12):980-997. doi: 10.1016/j.tins.2020.09.004. Epub 2020 Oct 19. Trends Neurosci. 2020. PMID: 33092893 Free PMC article. Review.
-
Exploration in neo-Hebbian reinforcement learning: Computational approaches to the exploration-exploitation balance with bio-inspired neural networks.Neural Netw. 2022 Jul;151:16-33. doi: 10.1016/j.neunet.2022.03.021. Epub 2022 Mar 23. Neural Netw. 2022. PMID: 35367735 Review.
Cited by
-
Dynamics Learning Rate Bias in Pigeons: Insights from Reinforcement Learning and Neural Correlates.Animals (Basel). 2024 Feb 1;14(3):489. doi: 10.3390/ani14030489. Animals (Basel). 2024. PMID: 38338131 Free PMC article.
-
An opponent striatal circuit for distributional reinforcement learning.bioRxiv [Preprint]. 2024 Jan 3:2024.01.02.573966. doi: 10.1101/2024.01.02.573966. bioRxiv. 2024. Update in: Nature. 2025 Mar;639(8055):717-726. doi: 10.1038/s41586-024-08488-5. PMID: 38260354 Free PMC article. Updated. Preprint.
-
Reward prediction error neurons implement an efficient code for reward.Nat Neurosci. 2024 Jul;27(7):1333-1339. doi: 10.1038/s41593-024-01671-x. Epub 2024 Jun 19. Nat Neurosci. 2024. PMID: 38898182
-
A multidimensional distributional map of future reward in dopamine neurons.Nature. 2025 Jun;642(8068):691-699. doi: 10.1038/s41586-025-09089-6. Epub 2025 Jun 4. Nature. 2025. PMID: 40468078
-
The functional form of value normalization in human reinforcement learning.Elife. 2023 Jul 10;12:e83891. doi: 10.7554/eLife.83891. Elife. 2023. PMID: 37428155 Free PMC article.
References
-
- Sutton RS, Barto AG. Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press; 1998.
MeSH terms
LinkOut - more resources
Full Text Sources

