Assembly of planar chiral superlattices from achiral building blocks
- PMID: 35864092
- PMCID: PMC9304327
- DOI: 10.1038/s41467-022-31868-2
Assembly of planar chiral superlattices from achiral building blocks
Abstract
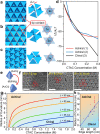
The spontaneous assembly of chiral structures from building blocks that lack chirality is fundamentally important for colloidal chemistry and has implications for the formation of advanced optical materials. Here, we find that purified achiral gold tetrahedron-shaped nanoparticles assemble into two-dimensional superlattices that exhibit planar chirality under a balance of repulsive electrostatic and attractive van der Waals and depletion forces. A model accounting for these interactions shows that the growth of planar structures is kinetically preferred over similar three-dimensional products, explaining their selective formation. Exploration and mapping of different packing symmetries demonstrates that the hexagonal chiral phase forms exclusively because of geometric constraints imposed by the presence of constituent tetrahedra with sharp tips. A formation mechanism is proposed in which the chiral phase nucleates from within a related 2D achiral phase by clockwise or counterclockwise rotation of tetrahedra about their central axis. These results lay the scientific foundation for the high-throughput assembly of planar chiral metamaterials.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures



Similar articles
-
Chiral Metal Nanoparticle Superlattices Enabled by Porphyrin-Based Supramolecular Structures.Angew Chem Int Ed Engl. 2021 Jun 21;60(26):14671-14678. doi: 10.1002/anie.202103809. Epub 2021 May 17. Angew Chem Int Ed Engl. 2021. PMID: 33843119
-
Chiral assemblies of pinwheel superlattices on substrates.Nature. 2022 Dec;612(7939):259-265. doi: 10.1038/s41586-022-05384-8. Epub 2022 Nov 28. Nature. 2022. PMID: 36443603
-
Achiral and chiral ligands synergistically harness chiral self-assembly of inorganics.Sci Adv. 2024 Oct 18;10(42):eado5948. doi: 10.1126/sciadv.ado5948. Epub 2024 Oct 18. Sci Adv. 2024. PMID: 39423258 Free PMC article.
-
Fabrication strategies for chiral self-assembly surface.Mikrochim Acta. 2024 Mar 16;191(4):202. doi: 10.1007/s00604-024-06278-4. Mikrochim Acta. 2024. PMID: 38492117 Review.
-
Recent Advances in Ultrathin Chiral Metasurfaces by Twisted Stacking.Adv Mater. 2023 Jan;35(3):e2206141. doi: 10.1002/adma.202206141. Epub 2022 Nov 29. Adv Mater. 2023. PMID: 36284479 Review.
Cited by
-
Concavity-enhanced chiral self-assembly of anisotropic nanoparticles toward strong chiroptical activity.Nat Commun. 2025 Jul 26;16(1):6897. doi: 10.1038/s41467-025-62165-3. Nat Commun. 2025. PMID: 40715080 Free PMC article.
-
Superstructural phase transitions in polymer-grafted nanooctahedra.Sci Adv. 2025 Jul 18;11(29):eadw2740. doi: 10.1126/sciadv.adw2740. Epub 2025 Jul 18. Sci Adv. 2025. PMID: 40680122 Free PMC article.
-
Coassembly of Complementary Polyhedral Metal-Organic Framework Particles into Binary Ordered Superstructures.J Am Chem Soc. 2024 Aug 7;146(31):21225-21230. doi: 10.1021/jacs.4c07194. Epub 2024 Jul 26. J Am Chem Soc. 2024. PMID: 39058575 Free PMC article.
-
DNA-mediated assembly of Au bipyramids into anisotropic light emitting kagome superlattices.Sci Adv. 2024 Jul 19;10(29):eadp3756. doi: 10.1126/sciadv.adp3756. Epub 2024 Jul 19. Sci Adv. 2024. PMID: 39028823 Free PMC article.
-
Rapid formation of gold core-satellite nanostructures using Turkevich-synthesized satellites and dithiol linkers: the do's and don'ts for successful assembly.Nanoscale Adv. 2024 May 31;6(14):3632-3643. doi: 10.1039/d4na00390j. eCollection 2024 Jul 9. Nanoscale Adv. 2024. PMID: 38989523 Free PMC article.
References
-
- Cecconello A, Besteiro LV, Govorov AO, Willner I. Chiroplasmonic DNA-based nanostructures. Nat. Rev. Mater. 2017;2:17039. doi: 10.1038/natrevmats.2017.39. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

