Beyond LIF Neurons on Neuromorphic Hardware

Abstract

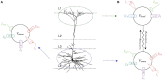
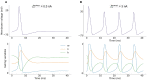
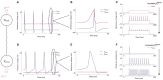
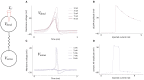
Neuromorphic systems aim to provide accelerated low-power simulation of Spiking Neural Networks (SNNs), typically featuring simple and efficient neuron models such as the Leaky Integrate-and-Fire (LIF) model. Biologically plausible neuron models developed by neuroscientists are largely ignored in neuromorphic computing due to their increased computational costs. This work bridges this gap through implementation and evaluation of a single compartment Hodgkin-Huxley (HH) neuron and a multi-compartment neuron incorporating dendritic computation on the SpiNNaker, and SpiNNaker2 prototype neuromorphic systems. Numerical accuracy of the model implementations is benchmarked against reference models in the NEURON simulation environment, with excellent agreement achieved by both the fixed- and floating-point SpiNNaker implementations. The computational cost is evaluated in terms of timing measurements profiling neural state updates. While the additional model complexity understandably increases computation times relative to LIF models, it was found a wallclock time increase of only 8× was observed for the HH neuron (11× for the mutlicompartment model), demonstrating the potential of hardware accelerators in the next-generation neuromorphic system to optimize implementation of complex neuron models. The benefits of models directly corresponding to biophysiological data are demonstrated: HH neurons are able to express a range of output behaviors not captured by LIF neurons; and the dendritic compartment provides the first implementation of a spiking multi-compartment neuron model with XOR-solving capabilities on neuromorphic hardware. The work paves the way for inclusion of more biologically representative neuron models in neuromorphic systems, and showcases the benefits of hardware accelerators included in the next-generation SpiNNaker2 architecture.

Keywords: Hodgkin-Huxley; SpiNNaker; dendritic computation; neuromorphic computing; neuronal modeling; spiking neural networks.

Figure 1

(A) Single-compartment HH model of a L2/L3 pyramidal neuron. The soma of the cell is modeled with a leak current, I_L, as well as sodium, I_Na, and potassium, I_K, currents. Current can be injected into the model, I_e, and it can receive multiple synaptic inputs, I_syn. (B) Two-compartment model of an L2/L3 pyramidal neuron consisting of a somatic and a dendritic compartment. The dendritic compartment incorporates a calcium ion channel current, I_Ca, and a leak current, I_L. The somatic compartment incorporates the same leak current, I_L, as well as sodium, I_Na, and potassium, I_K, currents. The compartments are connected by coupling conductances, g_soma,dend and g_dend,soma. Current can be injected into either compartment, I_e, and each compartment can receive multiple synaptic inputs, I_syn.

Figure 2

(A) Single-compartment model of a L2/L3 pyramidal neuron with injected current $I_e^{soma}$ = 0.3 nA and corresponding dimensionless ion-channel activation parameters m, n, and h which govern sodium, I_Na, and potassium, I_K, currents. (B) Current injection of $I_e^{soma}$ = 3 nA and corresponding m, n and h progression.

Figure 3

(A) Action potential initiation in dendritic and somatic compartment in response to a 3 nA injected current into the dendritic compartment. Dendritic compartment regularly fires dCaAPs with a refractory period of 200 ms. dCaAPs propagate to the somatic compartment and cause somatic action potentials. The dCaAP therefore precedes somatic action potentials (B). (C) Spiking dynamics of the dendritic compartment in response to increasing current injections into the dendrite, the frequency of dendritic spikes remains constant but the amplitude decreases as the current injection increases. (D) Action potential initiation in somatic compartment in response to a 10 nA injected current into the somatic compartment, the dendritic compartment does not fire in response to this injected current (E). (F) Spiking dynamics of the somatic compartment in response to increasing current injection into the soma, the frequency of somatic spikes increases as the current injection increases.

Figure 4

(A) Increasing injected current into the dendritic compartment results in a decrease in dCaAP amplitude. (B) The shape of the dCaAP is governed by the dendritic activation function, K(v) (Equation 10), which exhibits a characteristic shape in which the threshold current for dCaAP firing is the maximum dCaAP activation and hence the maximum dCaAP amplitude, the amplitude then decays with decay constant τ_K = 0.3 (dimensionless) (Equation 10). (C) Resulting somatic membrane voltage with increasing injected current into the dendritic compartment. Amplitude of somatic action potentials decreases with decreasing dCaAP amplitude. The all-or-nothing nature of these action potentials causes a lack of firing in the soma when the dendritic stimulus intensity gets higher. (D) Somatic action potential amplitudes are maximum when the dCaAP activation threshold is reached, they then decrease until the firing threshold for somatic action potentials is no longer reached and the soma stops firing.

Figure 5

Accuracy comparisons between the two-compartment model implemented on SpiNNaker, Jib2 and NEURON. The dendritic compartment fires a dCaAP in response to a current injection of 3.5nA which is accurately modeled on the neuromorphic platforms (A). The dendritic compartment is modeled accurately over time (B): absolute errors are small throughout the duration of the action potential and drop to 0 mV when the dendritic compartment enters its refractory period. In the somatic compartment, absolute errors are larger because the calculation of I_soma is voltage dependent, therefore when errors are produced in this calculation, an error in voltage is calculated which then, in turn, further increases the error in the I_soma calculations (C). Because of this, over time, SpiNNaker experiences accumulated errors. With Jib2 errors return to 0mV between spikes, and with do not accumulate over time (D).

Figure 6

Spiking properties of the somatic compartment. Shown are simulations of the two-compartment model with current injected into the somatic or dendritic compartment to reproduce different firing dynamics capturing a number of biologically representative neural capabilities. The firing dynamics in the box are achieved through injected current into the dendritic compartment rather than the somatic compartment itself. (A) Tonic spike. (B) Phasic spike. (C) Oscillations. (D) Accommodation. (E) Class II. (F) Rebound spike. (G) Integrator. (H) Variable threshold. (I) Adaptation. (J) XOR.

Figure 7

Somatic compartment exhibits XOR response to dendritic input in a single neuron model. (A) Dendritic and somatic firing dynamics in response to increased synaptic input into the dendritic compartment. Increased number of synapses leads to an initial increase and then decrease in dCaAP amplitude which subsequently cause the somatic compartment to start firing action potentials then stop. (B) The dynamics of the somatic compartment in response to the dendritic inputs provide a solution to the XOR problem in a single neuron model. Somatic compartment exhibits XOR response to dendritic input in a single neuron model. Increased number of synapses leads to an initial increase and then decrease in dCaAP amplitude which subsequently cause a similar increase and cease of somatic action potential firing.