Uncertainty quantification in cerebral circulation simulations focusing on the collateral flow: Surrogate model approach with machine learning
- PMID: 35867968
- PMCID: PMC9307280
- DOI: 10.1371/journal.pcbi.1009996
Uncertainty quantification in cerebral circulation simulations focusing on the collateral flow: Surrogate model approach with machine learning
Abstract
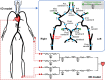
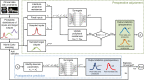
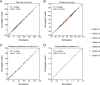
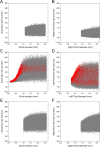
Collateral circulation in the circle of Willis (CoW), closely associated with disease mechanisms and treatment outcomes, can be effectively investigated using one-dimensional-zero-dimensional hemodynamic simulations. As the entire cardiovascular system is considered in the simulation, it captures the systemic effects of local arterial changes, thus reproducing collateral circulation that reflects biological phenomena. The simulation facilitates rapid assessment of clinically relevant hemodynamic quantities under patient-specific conditions by incorporating clinical data. During patient-specific simulations, the impact of clinical data uncertainty on the simulated quantities should be quantified to obtain reliable results. However, as uncertainty quantification (UQ) is time-consuming and computationally expensive, its implementation in time-sensitive clinical applications is considered impractical. Therefore, we constructed a surrogate model based on machine learning using simulation data. The model accurately predicts the flow rate and pressure in the CoW in a few milliseconds. This reduced computation time enables the UQ execution with 100 000 predictions in a few minutes on a single CPU core and in less than a minute on a GPU. We performed UQ to predict the risk of cerebral hyperperfusion (CH), a life-threatening condition that can occur after carotid artery stenosis surgery if collateral circulation fails to function appropriately. We predicted the statistics of the postoperative flow rate increase in the CoW, which is a measure of CH, considering the uncertainties of arterial diameters, stenosis parameters, and flow rates measured using the patients' clinical data. A sensitivity analysis was performed to clarify the impact of each uncertain parameter on the flow rate increase. Results indicated that CH occurred when two conditions were satisfied simultaneously: severe stenosis and when arteries of small diameter serve as the collateral pathway to the cerebral artery on the stenosis side. These findings elucidate the biological aspects of cerebral circulation in terms of the relationship between collateral flow and CH.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures






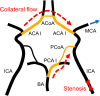
Similar articles
-
A computational model study of the influence of the anatomy of the circle of willis on cerebral hyperperfusion following carotid artery surgery.Biomed Eng Online. 2011 Sep 23;10:84. doi: 10.1186/1475-925X-10-84. Biomed Eng Online. 2011. PMID: 21943370 Free PMC article.
-
Circle of Willis Collateral During Temporary Internal Carotid Artery Occlusion II: Observations From Computed Tomography Angiography.Can J Neurol Sci. 2016 Jul;43(4):538-42. doi: 10.1017/cjn.2016.10. Epub 2016 Mar 31. Can J Neurol Sci. 2016. PMID: 27027491
-
Experimental study of hemodynamics in the Circle of Willis.Biomed Eng Online. 2015;14 Suppl 1(Suppl 1):S10. doi: 10.1186/1475-925X-14-S1-S10. Epub 2015 Jan 9. Biomed Eng Online. 2015. PMID: 25603138 Free PMC article.
-
Circle of Willis collateral flow investigated by magnetic resonance angiography.Stroke. 1999 Dec;30(12):2671-8. doi: 10.1161/01.str.30.12.2671. Stroke. 1999. PMID: 10582995 Review.
-
The clinical relevance of fetal variant of the circle of Willis and its influence on the cerebral collateral circulation.Acta Neurol Taiwan. 2011 Dec;20(4):232-42. Acta Neurol Taiwan. 2011. PMID: 22315173 Review.
Cited by
-
Uncertainty quantification of the pressure waveform using a Windkessel model.Int J Numer Method Biomed Eng. 2024 Dec;40(12):e3867. doi: 10.1002/cnm.3867. Epub 2024 Sep 6. Int J Numer Method Biomed Eng. 2024. PMID: 39239830 Free PMC article.
-
Development of a 3D Vascular Network Visualization Platform for One-Dimensional Hemodynamic Simulation.Bioengineering (Basel). 2024 Mar 26;11(4):313. doi: 10.3390/bioengineering11040313. Bioengineering (Basel). 2024. PMID: 38671739 Free PMC article.
-
A Computational Pipeline to Investigate Longitudinal Blood Flow Changes in the Circle of Willis of Patients with Stable and Growing Aneurysms.Ann Biomed Eng. 2024 Aug;52(8):2000-2012. doi: 10.1007/s10439-024-03493-1. Epub 2024 Apr 14. Ann Biomed Eng. 2024. PMID: 38616236 Free PMC article.
-
Computational modeling of multiscale collateral blood supply in a whole-brain-scale arterial network.PLoS Comput Biol. 2023 Sep 8;19(9):e1011452. doi: 10.1371/journal.pcbi.1011452. eCollection 2023 Sep. PLoS Comput Biol. 2023. PMID: 37683012 Free PMC article.
-
Aging and Sex Differences in Brain Volume and Cerebral Blood Flow.Aging Dis. 2024 Oct 1;15(5):2216-2229. doi: 10.14336/AD.2023.1122. Aging Dis. 2024. PMID: 38029394 Free PMC article.
References
-
- Smith NP, Pullan AJ, Hunter PJ. An anatomically based model of transient coronary blood flow in the heart. SIAM J Appl Math. 2002; 62(3):990–1018. 10.1137/S0036139999355199 - DOI
-
- Sherwin SJ, Franke V, Peiró J, Parker K. One-dimensional modelling of a vascular network in space-time variables. J Eng Math. 2003; 47(3):217–250. 10.1023/B:ENGI.0000007979.32871.e2 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials

