Computing transition path theory quantities with trajectory stratification
- PMID: 35868925
- PMCID: PMC9296190
- DOI: 10.1063/5.0087058
Computing transition path theory quantities with trajectory stratification
Abstract
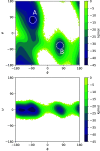
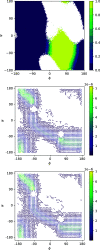
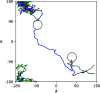
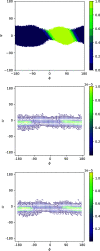
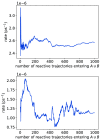
Transition path theory computes statistics from ensembles of reactive trajectories. A common strategy for sampling reactive trajectories is to control the branching and pruning of trajectories so as to enhance the sampling of low probability segments. However, it can be challenging to apply transition path theory to data from such methods because determining whether configurations and trajectory segments are part of reactive trajectories requires looking backward and forward in time. Here, we show how this issue can be overcome efficiently by introducing simple data structures. We illustrate the approach in the context of nonequilibrium umbrella sampling, but the strategy is general and can be used to obtain transition path theory statistics from other methods that sample segments of unbiased trajectories.
Figures


References
-
- Vanden-Eijnden E., “Transition path theory,” in Computer Simulations in Condensed Matter Systems: From Materials to Chemical Biology Volume 1, edited by Ferrario M., Ciccotti G., and Binder K. (Springer Berlin Heidelberg, Berlin, Heidelberg, 2006), pp. 453–493.
-
- E W. and Vanden-Eijnden E., “Towards a theory of transition paths,” J. Stat. Phys. 123, 503 (2006).10.1007/s10955-005-9003-9 - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

