Neurocomputational mechanisms of confidence in self and others

Abstract

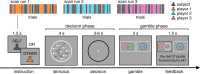
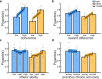
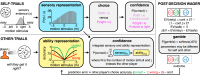
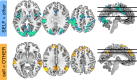
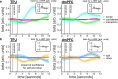
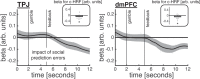
Computing confidence in one's own and others' decisions is critical for social success. While there has been substantial progress in our understanding of confidence estimates about oneself, little is known about how people form confidence estimates about others. Here, we address this question by asking participants undergoing fMRI to place bets on perceptual decisions made by themselves or one of three other players of varying ability. We show that participants compute confidence in another player's decisions by combining distinct estimates of player ability and decision difficulty - allowing them to predict that a good player may get a difficult decision wrong and that a bad player may get an easy decision right. We find that this computation is associated with an interaction between brain systems implicated in decision-making (LIP) and theory of mind (TPJ and dmPFC). These results reveal an interplay between self- and other-related processes during a social confidence computation.

Fig. 1. Social random dot motion task.

On each trial, participants placed a bet on a motion discrimination judgement (left or right) made by either themselves or one of three other players who varied in terms of their ability. The bet was made by choosing between a safe option, which yielded a small but guaranteed reward, and a risky option, which delivered a greater reward if the self- or other-choice was correct and a corresponding loss if incorrect. In this example, the participant chose the risky option (black box), but the self- or other-choice was incorrect. If participants chose the safe option, then they were informed what the outcome would have been had they selected the risky option. Participants were instructed how to calculate choice accuracy from the feedback screen. Participants were paired with the three other players in a block-wise manner, and the trial type was signalled at the start of a trial. For fMRI analysis, we refer to the time window from the onset of the motion stimulus to 3 s after the onset of the decision screen as the decision phase and the time window from the onset of the gamble screen to the offset of the feedback screen as the gamble phase.

Fig. 2. Behavioural results.

In each panel, data are split into self-trials (blue) and other-trials (yellow). a Probability gamble (i.e., proportion of trials in which the risky option was selected) as a function of coherence (median split). b Probability gamble as a function of the reward difference between the risky and the safe option (median split). c Probability gamble as a function of the ability of the other players. d Probability gamble as a function of choice accuracy on the previous trial of the same type. a–d Bar charts are empirical data, with individual participants overlaid as dots. Lines are data simulated under the best-fitting model (ToM-model). Empirical and simulated data are represented as group mean ± 95% CI, n = 21. Source data are provided as a Source Data file.

Fig. 3. Illustration of a confidence computation for self and others under the ToM-model.

All models assumed that participants’ choices and confidence were computed on self-trials according to Bayesian decision theory. Participants represent the stimulus space as comprised of a set of distinct motion stimuli, each defined by a direction (sign) and a coherence (absolute value). On each trial, participants receive sensory evidence sampled from a Gaussian distribution whose mean is given by the true motion stimulus and whose standard deviation is given by a participant’s sensory noise. Participants compute a belief state over the stimulus space given the sensory evidence and their sensory noise (blue box) and use this belief state to generate both a decision about the motion direction and their confidence in this decision being correct. The ToM-model assumes that participants compute confidence in others’ choices by combining their belief state over stimulus space with a representation of another player’s expected accuracy for each motion stimulus (yellow box). The latter representation – in effect, a psychometric function – is derived from an estimate of the other player’s sensory noise. This estimate is updated at the end of each trial using a Rescorla-Wagner learning rule that takes into account the accuracy of the other player’s choice and the confidence in this choice being correct. As a result of this update, the psychometric function becomes steeper after a correct choice (green) and shallower after an incorrect choice (red). On both trial types, confidence is used to calculate the difference in expected value between the risky and the safe options. Finally, the difference in expected value is entered into a softmax function to obtain the probability of selecting the risky option. The softmax parameters were allowed to vary between self- and other-trials.

Fig. 4. Whole-brain activations for self- and other-related processing during decision phase.

Images display clusters surviving whole-brain correction (p < 0.05, FWE-corrected for multiple comparisons at a cluster-defining threshold of p < 0.001, uncorrected) for the contrast between self- and other-trials during the decision phase (cold: SELF > other; warm: self < OTHER). Images are shown at p < 0.001, uncorrected. All clusters surviving whole-brain correction during the stimulus and gamble phases are detailed in Supplementary Tables 2 and 3.

Fig. 5. Anatomical masks for ROI analyses.

The MT+ mask was specified for each participant using a localiser scan. The other masks were specified using published connectivity-based parcellation atlases (see Methods).

Fig. 6. Encoding of motion coherence in MT+ and LIP.

a The time courses are coefficients from a regression in which we predicted z-scored MT+ (left) and LIP (right) activity time courses using trial type (cyan; other = 0.5; self = −0.5), z-scored motion coherence (pink) and their interaction (green). The insets show coefficients from an analysis of canonical HRFs (c-HRFs; asterisk indicates statistical significance, p < 0.05, one-sample t-test against zero). b Same approach as in a, but now quantifying the impact of motion coherence separately for each trial type. a–b Data are represented as group mean ± SEM, n = 21. Source data are provided as a Source Data file.

Fig. 7. TPJ and dmPFC support a social confidence computation.

a The time courses are coefficients from a regression in which we predicted z-scored TPJ (left) and dmPFC (right) activity time courses using trial type (cyan; other = 0.5; self = −0.5), z-scored model-based confidence estimates as computed under the ToM-model (pink; first orthogonalised with respect to motion coherence) and their interaction (green). The insets show coefficients from an analysis of canonical HRFs (c-HRFs; asterisk indicates statistical significance, p < 0.05, one-sample t-test against zero). b Same approach as in a, but now quantifying the impact of model-based confidence estimates separately for each trial type. a–b Data are represented as group mean ± SEM, n = 21. Source data are provided as a Source Data file.

Fig. 8. Functional coupling between sensory and social ROIs during a social confidence computation.

a Schematic of PPI analysis testing whether the correlation between LIP activity (seed region) and TPJ/dmPFC activity is higher on other- than self-trials. b Contrast estimates from PPI analysis (other > self) as implemented by the Generalised PPI toolbox (asterisk indicates statistical significance, p < 0.05, one-sample t-test against zero). c Visualisation of activity time courses driving effects documented in b. The time courses are coefficients from a regression in which we predicted z-scored TPJ/dmPFC activity time courses using an interaction between z-scored LIP activity time courses and trial type (self = −0.5; other = 0.5), while controlling for the main effect of each term. b–c Data are represented as group mean ± SEM, n = 21. Source data are provided as a Source Data file.

Fig. 9. Encoding of social prediction errors in TPJ and dmPFC.

The time courses are coefficients from a regression in which we predicted z-scored TPJ (left) and dmPFC (right) activity time courses using z-scored social prediction errors as computed under the best-fitting ToM-model. The insets show coefficients from an analysis of canonical HRFs (c-HRFs; asterisk indicates statistical significance, p < 0.05, one-sample t-test against zero). Data are represented as group mean ± SEM, n = 21. Source data are provided as a Source Data file.