A Continuum-Tensegrity Computational Model for Chondrocyte Biomechanics in AFM Indentation and Micropipette Aspiration

Abstract

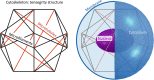
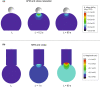
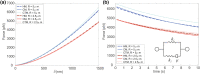
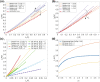
Mechanical stimuli are fundamental in the development of organs and tissues, their growth, regeneration or disease. They influence the biochemical signals produced by the cells, and, consequently, the development and spreading of a disease. Moreover, tumour cells are usually characterized by a decrease in the cell mechanical properties that may be directly linked to their metastatic potential. Thus, recently, the experimental and computational study of cell biomechanics is facing a growing interest. Various experimental approaches have been implemented to describe the passive response of cells; however, cell variability and complex experimental procedures may affect the obtained mechanical properties. For this reason, in-silico computational models have been developed through the years, to overcome such limitations, while proposing valuable tools to understand cell mechanical behaviour. This being the case, we propose a combined continuous-tensegrity finite element (FE) model to analyse the mechanical response of a cell and its subcomponents, observing how every part contributes to the overall mechanical behaviour. We modelled both Atomic Force Microscopy (AFM) indentation and micropipette aspiration techniques, as common mechanical tests for cells and elucidated also the role of cell cytoplasm and cytoskeleton in the global cell mechanical response.

Keywords: AFM indentation; Cell mechanics; Finite element model; Micropipette aspiration; Tensegrity.

Figure 1

Continuum-tensegrity model of the cell, where the lattice represents the cytoskeleton (with microfilaments in black and microtubules in red), while nucleus, membrane and cytoplasm are described as homogeneous materials.

Figure 2

Analyses steps. (a) AFM and stress relaxation: at time t₀ the rigid sphere indents the cell. After an average time of t₁ the maximum displacement is reached and stress relaxation begins. Few variations of stress distributions are visible after time t₂. Von Mises stresses distribution is reported with colormap and graduated scale (in MPa). (b) MPA and creep: at time t₀ the rigid micropipette is in contact with the cell. After t₁ the maximum negative pressure is applied and kept constant, to observe the creep behaviour of the cell until time t₂. Total cell displacement is reported with colormap and graduated scale (in nm).

Figure 3

Comparison between the Hertz analytical model (HM, dashed blue and red lines), the homogeneous continuum model with hyperelastic formulation (CM, full lines) and the continuum-tensegrity model (CTM, dotted lines) during AFM loading phase (a) and the stress relaxation phase (b). Two indenter sizes (R = 2.5 μm and 5 μm) were analysed with an indentation length of 1.5 μm. Mechanical parameter that were used for both the loading and stress-relaxation phases are reported in Tables 1 and 2.

Figure 4

(a) Comparison of different combinations of material properties for the cytoskeleton and the cytoplasm to observe the role of the tensegrity structure in the overall mechanical response of the model. Stiffer refers to the cell type 1 or 2 multiplied by Q, while softer states for cell type 1 or 2 divided by Q. The parameters of each curve are described in Table 3. (b) normalized results with respect to the maximum force obtained for both cell type 1 and 2.

Figure 5

(a) Comparison between incompressible (I) and compressible (C) models of the loading phase of a cell undergoing micropipette aspiration for different values of D_c/D_p. The curves from the work of Baaijens et al. are compared to the Half-Space analytical model (dashed line) and to our simulation (red line with stars). The cell diameter is fixed. (b) Dependence of the model by the Poisson’s ratio. Data from the work of Baaijens et al. are reported, compared with our simulation (red line with stars), and the Half-Space model with a dashed blue line. (c) Comparison of simulations of the loading phase of the micropipette aspiration employing different D_c/D_p ratios. Different colors highlight the ratios (blue for 1.5, light blue for 2, green for 3, yellow for 4 and red for 5.52) while different styles were used to identify our data and Baaijens et al. Data are normalized with respect to cell radius instead of micropipette radius. (d) Comparison between experimental data (from Baaijens et al.) and simulations by changing D_c/D_p.

Figure 6

(a) MPA on CTM with two analyzed configurations (1 and 2). (b) Aspiration length in time, with respect to the initial configuration of the cell cytoskeleton. A comparison with the CM is reported, as well as two different case studies with D_c/D_p equal to 2 and 3.