Permutation-Based Block Code for Short Packet Communication Systems

Abstract

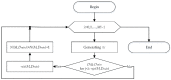
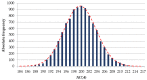
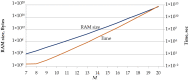
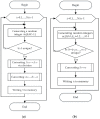
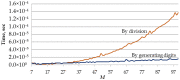
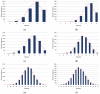
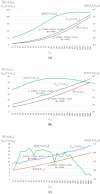
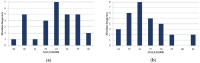
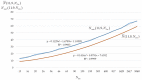
This paper presents an approach to the construction of block error-correcting code for data transmission systems with short packets. The need for this is driven by the necessity of information interaction between objects of machine-type communication network with a dynamically changing structure and unique system of commands or alerts for each network object. The codewords of a code are permutations with a given minimum pairwise Hamming distance. The purpose of the study is to develop a statistical method for constructing a code, in contrast to known algebraic methods, and to investigate the code size. An algorithm for generating codewords has been developed. It can be implemented both by enumeration of the full set of permutations, and by enumeration of a given number of randomly selected permutations. We have experimentally determined the dependencies of the average and the maximum values of the code size on the size of a subset of permutations used for constructing the code. A technique for computing approximation quadratic polynomials for the determined code size dependencies has been developed. These polynomials and their corresponding curves estimate the size of a code generated from a subset of random permutations of such a size that a statistically significant experiment cannot be performed. The results of implementing the developed technique for constructing a code based on permutations of lengths 7 and 11 have been presented. The prediction relative error of the code size did not exceed the value of 0.72% for permutation length 11, code distance 9, random permutation subset size 50,000, and permutation statistical study range limited by 5040.

Keywords: block error-correcting code; code size; codeword; factorial code; permutation; permutation code; secure channel coding scheme.

Figure 1

Algorithm to generate a set of codewords.

Figure 2

Algorithm to generate a set of codewords without storing the full set of permutations.

Figure 3

Histogram of the distribution of a random value $N\left(7,4\right)$.

Figure 4

The required amount of memory and time to generate a complete set of $M!$ permutations.

Figure 5

Algorithms to generate the initial set of $N_{lim}$ random permutations: (a) By division; (b) By generating digits.

Figure 6

The average time to generate one factorial number using two different algorithms.

Figure 7

Histograms of the distribution of a random variable $N\left(7,4,N_{lim}\right)$ for: (a) $N_{lim}=13$; (b) $N_{lim}=14$; (c) $N_{lim}=18$; (d) $N_{lim}=23$; (e) $N_{lim}=30$; (f) $N_{lim}=46$.

Figure 8

Graphs of $\overline{N}\left(M,D_{min},N_{lim}\right)$, $\sigma \left(N\left(M,D_{min},N_{lim}\right)\right)$ and $N_{max}\left(M,D_{min},N_{lim}\right)$ for $M=7$ and: (a) $D_{min}=4$; (b) $D_{min}=5$; (c) $D_{min}=6$.

Figure 9

Graphs $\overline{N}\left(11,9,N_{lim}\right)$ and $N_{max}\left(11,9,N_{lim}\right)$ when $\mathsf{\Delta }=0.04$.

Figure 10

Histograms of the distribution of a random value $N\left(11,9,N_{lim}\right)$ for: (a) $N_{lim}=30,000$; (b) $N_{lim}=50,000$.

Figure 11

Graphs $\overline{N}\left(11,9,N_{lim}\right)$ and $N_{max}\left(11,9,N_{lim}\right)$ when $\mathsf{\Delta }=0.08$.