Rapid discovery of stable materials by coordinate-free coarse graining

Abstract

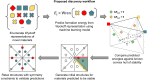
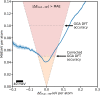
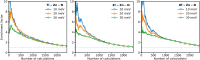
A fundamental challenge in materials science pertains to elucidating the relationship between stoichiometry, stability, structure, and property. Recent advances have shown that machine learning can be used to learn such relationships, allowing the stability and functional properties of materials to be accurately predicted. However, most of these approaches use atomic coordinates as input and are thus bottlenecked by crystal structure identification when investigating previously unidentified materials. Our approach solves this bottleneck by coarse-graining the infinite search space of atomic coordinates into a combinatorially enumerable search space. The key idea is to use Wyckoff representations, coordinate-free sets of symmetry-related positions in a crystal, as the input to a machine learning model. Our model demonstrates exceptionally high precision in finding unknown theoretically stable materials, identifying 1569 materials that lie below the known convex hull of previously calculated materials from just 5675 ab initio calculations. Our approach opens up fundamental advances in computational materials discovery.

Fig. 1.. Coarse-graining materials space using Wyckoff representations enables efficient data-driven materials discovery.

A machine learning–powered materials discovery workflow that takes advantage of the benefits of the proposed Wyckoff representation. The workflow uses a machine learning model to predict formation energies for candidate materials in an enumerated library of Wyckoff representations (shapes are used to denote different Wyckoff positions and colors to denote different element types). These predicted formation energies are then compared against the known convex hull of stability. Structures satisfying the required symmetries are then generated and relaxed for materials predicted to be stable. The calculated energies of the relaxed structures can then be compared against the known convex hull to confirm whether the candidate is stable.

Fig. 2.. Wren’s average error is below DFT error in the region around the stability threshold.

Rolling mean absolute error (MAE) on the WBM dataset as the energy to the convex hull is varied for Wren model. A scale bar is shown for the windowing period of 40 meV per atom used when calculating the rolling average. The SEM is shaded around each curve. The highlighted V-shaped region shows the area in which the average absolute error is greater than the energy to the known convex hull; this is the region where the model is most at risk of misclassifying structures. In most of this region, Wren’s accuracy is well below the threshold of 100 meV per atom considered to be the accuracy of semilocal DFT across diverse chemistries (66) and comparable to the threshold of ∼50 meV per atom characteristic of fitted correction schemes (–69).

Fig. 3.. Wren accelerates the recovery of low-energy structures in unseen chemical systems.

The figures show how the enrichment factor varies as we use Wren to direct the exploration of the Ti-Zn-N, Zr-Zn-N, and Hf-Zn-N chemical systems. The enrichment factor is the ratio of candidates found satisfying a given triage criterion to the number we would expect to find via a random search. The enrichment factor is plotted for candidates within 10, 20, and 30 meV per atom from the convex hull of the full explored system. A light-gray guideline is included to show the performance expected from a random model, an enrichment factor of 1. The plots demonstrate that using Wren leads to a significant degree of early enrichment of low-energy structures.

Fig. 4.. Wren enables automated computational prospecting of previously unidentified stable materials.

Data-mined substitution probabilities are used to generate candidates for screening. A heatmap of the data-mined log substitution probabilities for the first 36 main group elements is shown in the top left. The matrix captures known chemical trends, for example, that halogens can often be substituted for each other in crystal structures. Using the Wren allows far more unrelaxed candidates to be considered than possible in conventional DFT-led high-throughput workflows. The funnel diagram shows the number of unrelaxed candidates that pass the different stability criteria when filtering based on the predictions of the Wren model. In total, 4721 of 5675 validation calculations completed. Of these, 1569 were below the known convex hull, giving a precision of 33% among the completed calculations.

Fig. 5.. Breakdown of different components of the Wyckoff position embeddings.

The Wyckoff position embeddings are made up of two parts: first, the Wyckoff proportion of the embedding that is composed of three subsections encoding the crystal system, Bravais centering, and equivalent sites in the Wyckoff positions; second, the elemental embedding for which we take the matscholar embedding from (48).

Fig. 6.. On-the-fly augmentation of equivalent Wyckoff representations ensures invariance to equivalent descriptions.

The labeling of Wyckoff positions includes a choice of setting; to ensure that our model is invariant to these choices, we perform on-the-fly augmentation of all equivalent Wyckoff representations and then average the augmented embeddings before they are fed into the output network.