A device-independent quantum key distribution system for distant users

Abstract

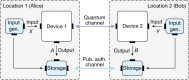
Device-independent quantum key distribution (DIQKD) enables the generation of secret keys over an untrusted channel using uncharacterized and potentially untrusted devices^1-9. The proper and secure functioning of the devices can be certified by a statistical test using a Bell inequality^10-12. This test originates from the foundations of quantum physics and also ensures robustness against implementation loopholes¹³, thereby leaving only the integrity of the users' locations to be guaranteed by other means. The realization of DIQKD, however, is extremely challenging-mainly because it is difficult to establish high-quality entangled states between two remote locations with high detection efficiency. Here we present an experimental system that enables for DIQKD between two distant users. The experiment is based on the generation and analysis of event-ready entanglement between two independently trapped single rubidium atoms located in buildings 400 metre apart¹⁴. By achieving an entanglement fidelity of [Formula: see text] and implementing a DIQKD protocol with random key basis¹⁵, we observe a significant violation of a Bell inequality of S = 2.578(75)-above the classical limit of 2-and a quantum bit error rate of only 0.078(9). For the protocol, this results in a secret key rate of 0.07 bits per entanglement generation event in the asymptotic limit, and thus demonstrates the system's capability to generate secret keys. Our results of secure key exchange with potentially untrusted devices pave the way to the ultimate form of quantum secure communications in future quantum networks.

Fig. 1. Schematic of a DIQKD scheme.

Each of the two parties, Alice and Bob, holds QKD devices, which are connected by a quantum channel. The devices receive the inputs X and Y, and respond with outputs A and B, respectively. To run the protocol each party needs a trusted supply of inputs and a trusted local storage unit to store both output and inputs. Additionally, a trusted authenticated public channel (pub. auth. channel) between the two parties is necessary for exchange of information during post-processing. gen., generation.

Fig. 2. Overview of the DIQKD system.

a, Alice’s equipment (Device 1 in Lab 1) is formed by a single-atom trap and a BSM set-up. Bob (Device 2 in Lab 2) uses a second single-atom trap together with a 90:10 (T:R) beam splitter (BS) and a single-photon detector (SPD). Each trap set-up contains a high numerical aperture (NA) objective to optically trap a single atom and collect atomic fluorescence into a single-mode (SM) fibre. The atoms are entangled in an event-ready scheme by synchronously exciting them, after which the spontaneously emitted photons are collected by high-NA objectives and guided to the BSM. Here, a coincidental photon detection on two detectors in the same output arm of the fibre BS heralds the entangled atom–atom state $|{\mathrm{\Psi }}^{+}⟩$, which is announced to both users by a ‘ready’ signal. After receiving the ready signal, two quantum random number generators (QRNGs) select the inputs to the devices, determining the polarization of a read-out pulse in a state-selective ionization scheme. The binary output of the devices is determined from a fluorescence measurement of atom presence after the ionization attempt, as ionized atoms are lost from the trap. The inputs and outputs of each round are stored locally using a trusted storage. In Lab 2 a spectral filter and shutter are implemented to avoid leakage of the inputs and outputs of the device. b, Map showing the main campus of the LMU in Munich, indicating the locations of the two laboratories. Map data in b are from Bayerische Vermessungsverwaltung .

Fig. 3. Schematics of the entanglement generation and atomic-state read-out schemes.

a, An entangled atom–photon state is generated by the spontaneous emission of a photon subsequent to excitation of the atom. Decay from the state $5^2{\mathrm{P}}_{3/2}|F\prime =0,m_{F^{\prime }}=0⟩$ results in an entangled atom–photon state ${\mid \mathrm{\Psi }⟩}_{AP}=1/\sqrt{2}\left({\mid \downarrow ⟩}_x\mid H⟩+{\mid \uparrow ⟩}_x\mid V⟩\right)$, where ${|\uparrow ⟩}_x≔1/\sqrt{2}\left({|\uparrow ⟩}_z+{|\downarrow ⟩}_z\right)$ (respectively ${|\downarrow ⟩}_x≔i/\sqrt{2}\left({|\uparrow ⟩}_z-{|\downarrow ⟩}_z\right)$) and $|H⟩$ and $|V⟩$ denote parallel and orthogonal linear polarizations with respect to the optical table, respectively, with $|V⟩≔1/\sqrt{2}\left(|L⟩+|R⟩\right)$ and $|H⟩≔i/\sqrt{2}\left(|L⟩-|R⟩\right)$. b, The atomic qubit state is read out by a state-dependent ionization scheme. First, a certain superposition of the qubit state is excited to the 5²P_1/2 level depending on a respective polarization of the so-called read-out laser light (λ = 795 nm). The excited atom is ionized by a bright second laser applied simultaneously at λ = 473 nm. If the atom decays to the state $5^2{\mathrm{S}}_{1/2}|F=2⟩$ before it is ionized, it is excited to the state $5^2{\mathrm{P}}_{3/2}|F\prime =3⟩$ with the third excitation laser at λ = 780 nm, which is ionized as well.

Fig. 4. Atom–atom state correlations.

The correlations E_X,Y are obtained from the correlation (blue) and anticorrelation (red) probabilities of the device outputs for the eight input combinations. The data are fitted with sinusoidal functions estimating visibilities of 0.869(25) and 0.888(45). The settings for X = 2 or X = 3 (green background) contribute to the evaluation of the Bell parameter S = 2.578(75), whereas the QBER Q = 0.078(9) follows from settings with X = Y (yellow background). The error bars indicate statistical errors of one standard deviation. N = 3,342.

Fig. 5. Finite-key simulation for the robust DIQKD protocol.

Shown is the minimum number of rounds, that is, block length, required to distribute a finite key with a certain epsilon security, considering collective attacks and uniformly distributed measurement settings. The channel parameters S, Q₀ and Q₁ are set to the observed values in the experiment. A non-asymptotic security of ε_DI = 10⁻⁵ is considered to be realistic for cryptography applications.