Diverging from the Norm: Reevaluating What Miniature Excitatory Postsynaptic Currents Tell Us about Homeostatic Synaptic Plasticity
- PMID: 35904350
- PMCID: PMC12216122
- DOI: 10.1177/10738584221112336
Diverging from the Norm: Reevaluating What Miniature Excitatory Postsynaptic Currents Tell Us about Homeostatic Synaptic Plasticity
Abstract
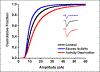
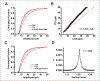
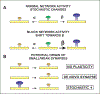
The idea that the nervous system maintains a set point of network activity and homeostatically returns to that set point in the face of dramatic disruption-during development, after injury, in pathologic states, and during sleep/wake cycles-is rapidly becoming accepted as a key plasticity behavior, placing it alongside long-term potentiation and depression. The dramatic growth in studies of homeostatic synaptic plasticity of miniature excitatory synaptic currents (mEPSCs) is attributable, in part, to the simple yet elegant mechanism of uniform multiplicative scaling proposed by Turrigiano and colleagues: that neurons sense their own activity and globally multiply the strength of every synapse by a single factor to return activity to the set point without altering established differences in synaptic weights. We have recently shown that for mEPSCs recorded from control and activity-blocked cultures of mouse cortical neurons, the synaptic scaling factor is not uniform but is close to 1 for the smallest mEPSC amplitudes and progressively increases as mEPSC amplitudes increase, which we term divergent scaling. Using insights gained from simulating uniform multiplicative scaling, we review evidence from published studies and conclude that divergent synaptic scaling is the norm rather than the exception. This conclusion has implications for hypotheses about the molecular mechanisms underlying synaptic scaling.
Keywords: activity dependent; divergent scaling; homeostatic; homeostatic plasticity; homeostatic synaptic plasticity; mEPSCs; mEPSPs; synaptic; synaptic homeostasis; synaptic scaling.
Conflict of interest statement
Declaration of Conflicting InterestsThe authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Figures

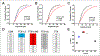


Similar articles
-
The interplay between homeostatic synaptic scaling and homeostatic structural plasticity maintains the robust firing rate of neural networks.Elife. 2025 Jul 4;12:RP88376. doi: 10.7554/eLife.88376. Elife. 2025. PMID: 40613658 Free PMC article.
-
Divergent Synaptic Scaling of Miniature EPSCs following Activity Blockade in Dissociated Neuronal Cultures.J Neurosci. 2020 May 20;40(21):4090-4102. doi: 10.1523/JNEUROSCI.1393-19.2020. Epub 2020 Apr 20. J Neurosci. 2020. PMID: 32312887 Free PMC article.
-
MDGA2 Constrains Glutamatergic Inputs Selectively onto CA1 Pyramidal Neurons to Optimize Neural Circuits for Plasticity, Memory, and Social Behavior.Neurosci Bull. 2024 Jul;40(7):887-904. doi: 10.1007/s12264-023-01171-1. Epub 2024 Feb 6. Neurosci Bull. 2024. PMID: 38321347 Free PMC article.
-
A rapid and systematic review of the clinical effectiveness and cost-effectiveness of paclitaxel, docetaxel, gemcitabine and vinorelbine in non-small-cell lung cancer.Health Technol Assess. 2001;5(32):1-195. doi: 10.3310/hta5320. Health Technol Assess. 2001. PMID: 12065068
-
How lived experiences of illness trajectories, burdens of treatment, and social inequalities shape service user and caregiver participation in health and social care: a theory-informed qualitative evidence synthesis.Health Soc Care Deliv Res. 2025 Jun;13(24):1-120. doi: 10.3310/HGTQ8159. Health Soc Care Deliv Res. 2025. PMID: 40548558
Cited by
-
Enhanced Synaptic Inhibition in the Dorsolateral Geniculate Nucleus in a Mouse Model of Glaucoma.eNeuro. 2024 Jul 11;11(7):ENEURO.0263-24.2024. doi: 10.1523/ENEURO.0263-24.2024. Print 2024 Jul. eNeuro. 2024. PMID: 38937109 Free PMC article.
-
GABAergic synaptic scaling is triggered by changes in spiking activity rather than AMPA receptor activation.Elife. 2024 Jun 28;12:RP87753. doi: 10.7554/eLife.87753. Elife. 2024. PMID: 38941139 Free PMC article.
-
Homeostatic Synaptic Plasticity of Miniature Excitatory Postsynaptic Currents in Mouse Cortical Cultures Requires Neuronal Rab3A.bioRxiv [Preprint]. 2025 Mar 21:2023.06.14.544980. doi: 10.1101/2023.06.14.544980. bioRxiv. 2025. PMID: 39071374 Free PMC article. Preprint.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

