Analysis of a diffusive epidemic system with spatial heterogeneity and lag effect of media impact
- PMID: 35913603
- PMCID: PMC9340761
- DOI: 10.1007/s00285-022-01780-w
Analysis of a diffusive epidemic system with spatial heterogeneity and lag effect of media impact
Abstract
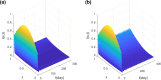
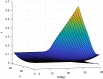
We considered an SIS functional partial differential model cooperated with spatial heterogeneity and lag effect of media impact. The wellposedness including existence and uniqueness of the solution was proved. We defined the basic reproduction number and investigated the threshold dynamics of the model, and discussed the asymptotic behavior and monotonicity of the basic reproduction number associated with the diffusion rate. The local and global Hopf bifurcation at the endemic steady state was investigated theoretically and numerically. There exists numerical cases showing that the larger the number of basic reproduction number, the smaller the final epidemic size. The meaningful conclusion generalizes the previous conclusion of ordinary differential equation.
Keywords: Functional partial differential model; Hopf bifurcation; Media impact; Spatial heterogeneity.
© 2022. The Author(s), under exclusive licence to Springer-Verlag GmbH Germany, part of Springer Nature.
Figures

Similar articles
-
Global Hopf bifurcation analysis of an susceptible-infective-removed epidemic model incorporating media coverage with time delay.J Biol Dyn. 2017 Dec;11(1):8-24. doi: 10.1080/17513758.2016.1229050. J Biol Dyn. 2017. PMID: 27627694
-
Analysis of an Epidemic System with Two Response Delays in Media Impact Function.Bull Math Biol. 2019 May;81(5):1582-1612. doi: 10.1007/s11538-019-00586-0. Epub 2019 Feb 20. Bull Math Biol. 2019. PMID: 30788689
-
Analysis of cholera epidemics with bacterial growth and spatial movement.J Biol Dyn. 2015;9 Suppl 1:233-61. doi: 10.1080/17513758.2014.974696. Epub 2014 Nov 3. J Biol Dyn. 2015. PMID: 25363286
-
Qualitative analysis of a class of SISM epidemic model influenced by media publicity.Math Biosci Eng. 2020 Aug 28;17(5):5727-5751. doi: 10.3934/mbe.2020308. Math Biosci Eng. 2020. PMID: 33120575
-
Bifurcation analysis of a pair-wise epidemic model on adaptive networks.Math Biosci Eng. 2019 Apr 10;16(4):2973-2989. doi: 10.3934/mbe.2019147. Math Biosci Eng. 2019. PMID: 31137246
Cited by
-
A modelling approach to characterise the interaction between behavioral response and epidemics: A study based on COVID-19.Infect Dis Model. 2024 Dec 26;10(2):477-492. doi: 10.1016/j.idm.2024.12.013. eCollection 2025 Jun. Infect Dis Model. 2024. PMID: 39845730 Free PMC article.
-
Role of limited medical resources in an epidemic model with media report and general birth rate.Infect Dis Model. 2025 Jan 7;10(2):522-535. doi: 10.1016/j.idm.2025.01.001. eCollection 2025 Jun. Infect Dis Model. 2025. PMID: 39876982 Free PMC article.
References
-
- Allen LJS, Bolker BM, Lou Y, Nevai AL. Asymptotic profiles of the steady states for an SIS epidemic reaction-diffusion model. Discrete Contin Dyn Syst Ser A. 2008;21(1):1–20. doi: 10.3934/dcds.2008.21.1. - DOI
-
- Anderson RM, May RM (1991) Infectious Diseases of Humans: Dynamics and Control. Cambridge University Press
-
- Busenberg S, Huang W. Stability and Hopf bifurcation for a population delay model with diffusion effects. J Differ Equ. 1996;124(1):80–107. doi: 10.1006/jdeq.1996.0003. - DOI
-
- Cantrell RS, Cosner C (2003) Spatial Ecology via Reaction-diffusion Equations. John Wiley and Sons Ltd, Chichester
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

