Analysis of a diffusive epidemic system with spatial heterogeneity and lag effect of media impact

Abstract

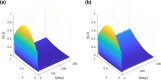
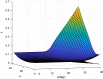
We considered an SIS functional partial differential model cooperated with spatial heterogeneity and lag effect of media impact. The wellposedness including existence and uniqueness of the solution was proved. We defined the basic reproduction number and investigated the threshold dynamics of the model, and discussed the asymptotic behavior and monotonicity of the basic reproduction number associated with the diffusion rate. The local and global Hopf bifurcation at the endemic steady state was investigated theoretically and numerically. There exists numerical cases showing that the larger the number of basic reproduction number, the smaller the final epidemic size. The meaningful conclusion generalizes the previous conclusion of ordinary differential equation.

Keywords: Functional partial differential model; Hopf bifurcation; Media impact; Spatial heterogeneity.

Fig. 1

(a) The epidemic size $H_I$ of system (2) with respect to $d_I$ under ${\mathcal{R}}_0<1$. Parameters are fixed as (37). (b) The epidemic size $H_I$ with respect to $d_I$ under ${\mathcal{R}}_0>1$ Parameters are fixed as (38)

Fig. 2

Solutions of system (17) showing that (A) the endemic steady state is asymptotically stable for $r=6.4<r_0\approx 6.4$, and (B) the bifurcated periodic solution is feasible for $r=6.8>r_0\approx 6.4$. Parameters are fixed as (39)

Fig. 3

Bifurcation diagram describing the dynamics of system (17) as r increases. Parameters are fixed as (39)