The role of mitochondrial energetics in the origin and diversification of eukaryotes
- PMID: 35915152
- PMCID: PMC9575660
- DOI: 10.1038/s41559-022-01833-9
The role of mitochondrial energetics in the origin and diversification of eukaryotes
Abstract
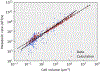
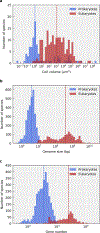
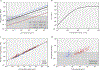
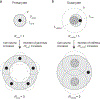
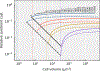
The origin of eukaryotic cell size and complexity is often thought to have required an energy excess supplied by mitochondria. Recent observations show energy demands to scale continuously with cell volume, suggesting that eukaryotes do not have higher energetic capacity. However, respiratory membrane area scales superlinearly with the cell surface area. Furthermore, the consequences of the contrasting genomic architectures between prokaryotes and eukaryotes have not been precisely quantified. Here, we investigated (1) the factors that affect the volumes at which prokaryotes become surface area-constrained, (2) the amount of energy divested to DNA due to contrasting genomic architectures and (3) the costs and benefits of respiring symbionts. Our analyses suggest that prokaryotes are not surface area-constrained at volumes of 100‒103 µm3, the genomic architecture of extant eukaryotes is only slightly advantageous at genomes sizes of 106‒107 base pairs and a larger host cell may have derived a greater advantage (lower cost) from harbouring ATP-producing symbionts. This suggests that eukaryotes first evolved without the need for mitochondria since these ranges hypothetically encompass the last eukaryotic common ancestor and its relatives. Our analyses also show that larger and faster-dividing prokaryotes would have a shortage of respiratory membrane area and divest more energy into DNA. Thus, we argue that although mitochondria may not have been required by the first eukaryotes, eukaryote diversification was ultimately dependent on mitochondria.
© 2022. The Author(s), under exclusive licence to Springer Nature Limited.
Conflict of interest statement
Competing Interests Statement
The authors declare no competing interests.
Figures

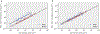


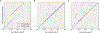

Similar articles
-
Energetics and genetics across the prokaryote-eukaryote divide.Biol Direct. 2011 Jun 30;6:35. doi: 10.1186/1745-6150-6-35. Biol Direct. 2011. PMID: 21714941 Free PMC article.
-
Origin and Early Evolution of the Eukaryotic Cell.Annu Rev Microbiol. 2021 Oct 8;75:631-647. doi: 10.1146/annurev-micro-090817-062213. Epub 2021 Aug 3. Annu Rev Microbiol. 2021. PMID: 34343017
-
Membranes, energetics, and evolution across the prokaryote-eukaryote divide.Elife. 2017 Mar 16;6:e20437. doi: 10.7554/eLife.20437. Elife. 2017. PMID: 28300533 Free PMC article.
-
Was the Mitochondrion Necessary to Start Eukaryogenesis?Trends Microbiol. 2019 Feb;27(2):96-104. doi: 10.1016/j.tim.2018.10.005. Epub 2018 Nov 19. Trends Microbiol. 2019. PMID: 30466901 Review.
-
Energetics and evolution of anaerobic microbial eukaryotes.Nat Microbiol. 2023 Feb;8(2):197-203. doi: 10.1038/s41564-022-01299-2. Epub 2023 Jan 16. Nat Microbiol. 2023. PMID: 36646908 Review.
Cited by
-
The emerging view on the origin and early evolution of eukaryotic cells.Nature. 2024 Sep;633(8029):295-305. doi: 10.1038/s41586-024-07677-6. Epub 2024 Sep 11. Nature. 2024. PMID: 39261613 Review.
-
The origin of eukaryotes and rise in complexity were synchronous with the rise in oxygen.Front Bioinform. 2023 Sep 1;3:1233281. doi: 10.3389/fbinf.2023.1233281. eCollection 2023. Front Bioinform. 2023. PMID: 37727796 Free PMC article.
-
The Anatomical and Evolutionary Impact of Pain, Pleasure, Motivation, and Cognition: Integrating Energy Metabolism and the Mind-Body BERN (Behavior, Exercise, Relaxation, and Nutrition) Framework.Int J Mol Sci. 2025 Jun 8;26(12):5491. doi: 10.3390/ijms26125491. Int J Mol Sci. 2025. PMID: 40564954 Free PMC article. Review.
-
Update on the correlation between mitochondrial function and osteonecrosis of the femoral head osteocytes.Redox Rep. 2025 Dec;30(1):2491846. doi: 10.1080/13510002.2025.2491846. Epub 2025 Apr 18. Redox Rep. 2025. PMID: 40249372 Free PMC article. Review.
-
Minimal Out-of-Equilibrium Metabolism for Synthetic Cells: A Membrane Perspective.ACS Synth Biol. 2023 Apr 21;12(4):922-946. doi: 10.1021/acssynbio.3c00062. Epub 2023 Apr 7. ACS Synth Biol. 2023. PMID: 37027340 Free PMC article. Review.
References
-
- Stanier RY, Douderoff M. & Adelberg E. The microbial world. (Prentice-Hall, 1963).
-
- Lane N. & Martin W. The energetics of genome complexity. Nature 467, 929–934 (2010). - PubMed
-
- Martin W. & Müller M. The hydrogen hypothesis for the first eukaryote. Nature 392, 37–41 (1998). - PubMed
-
- Cavalier-Smith T. Predation and eukaryote cell origins: A coevolutionary perspective. The International Journal of Biochemistry & Cell Biology 41, 307–322 (2009). - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

