Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 May 17:2022:2357258.
doi: 10.1155/2022/2357258. eCollection 2022.

An Elementary Solution to a Duffing Equation

Alvaro H Salas  1
Affiliations

An Elementary Solution to a Duffing Equation

Alvaro H Salas. ScientificWorldJournal. .

Abstract

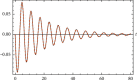
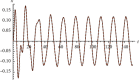
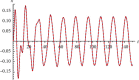
In this work, we study the Duffing equation. Analytical solution for undamped and unforced case is provided for any given arbitrary initial conditions. An approximate analytical solution is given for the damped or trigonometrically forced Duffing equation for arbitrary initial conditions. The analytical solutions are expressed in terms of elementary trigonometric functions as well as in terms of the Jacobian elliptic functions. Examples are added to illustrate the obtained results. We also introduce new functions for approximating the Jacobian and Weierstrass elliptic functions in terms of the trigonometric functions sine and cosine. Results are high accurate.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no conflicts of interest.

Figures

Figure 1
Figure 1
Comparison between the exact solution and the numerical solution for Example 1.
Figure 2
Figure 2
Comparison between the exact solution and the numerical solution for Example 2.
Figure 3
Figure 3
Comparison between the exact solution and the approximate analytical solution for Example 3.
Figure 4
Figure 4
Comparison between the exact solution and the approximate analytical solution for Example 4.
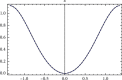
Figure 5
Figure 5
Comparison between the approximate analytical solution and the numerical solution for Example 5.
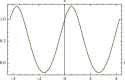
Figure 6
Figure 6
Comparison between the approximate analytical solution and the numerical solution for Example 6.
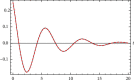
Figure 7
Figure 7
Comparison between the approximate analytical solution and the numerical solution for Example 7.
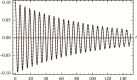
Figure 8
Figure 8
Comparison between the approximate analytical solution and the numerical solution for Example 8.
Figure 9
Figure 9
Comparison between the approximate analytical solution and the numerical solution for Example 9.
Figure 10
Figure 10
Comparison between the approximate analytical solution and the numerical solution for Example 10.
Figure 11
Figure 11
Comparison between the approximate analytical solution and the homotopy solution for Example 10.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Duffing G. Erzwungene Schwingung bei veränderlicher Eigenfrequenz und ihre technische Bedeutung . Braunschweig, Germany: Vieweg; 1918.
    1. Feng Z. A qualitative study of the damped duffing equation andApplications. Discrete and continuous dynamical systems-series B. Follow journal . 5(5) doi: 10.3934/dcdsb.2006.6.1097. - DOI
    1. Loria A., Panteley E., Nijmeijer H. Control of the chaotic Duffing equation withuncertainty in all parameters. IEEE Transactions on Circuits and Systems I . 1998;45(12):1252–1255. doi: 10.1109/81.736558. - DOI
    1. Thompson J. M. T., Stewart H. B. Nonlinear Dynamics and Chaos . New York, NY, USA: John Wiley & Sons; 1986.
    1. Moon F. C. Chaotic Vibrations: An Introduction for Applied Scientists and Engineers . New York, NY, USA: John Wiley & Sons; 1987.

LinkOut - more resources