Circular-linear copulae for animal movement data

Abstract

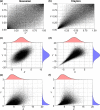
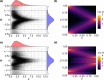
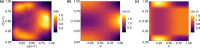
Animal movement is often modelled in discrete time, formulated in terms of steps taken between successive locations at regular time intervals. Steps are characterized by the distance between successive locations (step lengths) and changes in direction (turn angles). Animals commonly exhibit a mix of directed movements with large step lengths and turn angles near 0 when travelling between habitat patches and more wandering movements with small step lengths and uniform turn angles when foraging. Thus, step lengths and turn angles will typically be cross-correlated.Most models of animal movement assume that step lengths and turn angles are independent, likely due to a lack of available alternatives. Here, we show how the method of copulae can be used to fit multivariate distributions that allow for correlated step lengths and turn angles.We describe several newly developed copulae appropriate for modelling animal movement data and fit these distributions to data collected on fishers (Pekania pennanti). The copulae are able to capture the inherent correlation in the data and provide a better fit than a model that assumes independence. Further, we demonstrate via simulation that this correlation can impact movement patterns (e.g. rates of dispersion overtime).We see many opportunities to extend this framework (e.g. to consider autocorrelation in step attributes) and to integrate it into existing frameworks for modelling animal movement and habitat selection. For example, copulae could be used to more accurately sample available locations when conducting habitat-selection analyses.

FIGURE 1

Left: Scatter plot of step lengths ($x$, in meters) and turn angles ($\theta$) of six fishers from (LaPoint et al., 2013a, 2013b). Kernel density approximations of the marginal densities are plotted in red and blue next to the axes. The step lengths are separated into five quantiles as marked by the colour bar below the x‐axis. Right: Circular box plots of the same data. For each of the five step length quantiles, a box plot of the corresponding angles is shown. The sample medians are defined as the centre of the shortest arc that connects all points; in other words, the angle around which the spread of the data is minimal. Outliers, that is values outside 1.5 times the inter quartile range, are marked in red

FIGURE 2

Samples from copulae and corresponding joint distributions with non‐uniform margins. Left column: Gaussian copula with $\rho =0.6$. Right column: Clayton copula with $\alpha =3$. First row: samples drawn from the copulae. Second row: samples drawn from the joint distribution obtained with the corresponding copula and normal margins with means 0 and standard deviations 2 and 5. Third row: samples drawn from the joint distribution obtained with the corresponding copula, a marginal gamma distribution with shape = 5 and scale = 1 (x‐direction) and marginal exponential distribution with rate = 3 (y‐direction)

FIGURE 3

Left: linear ($x$) and circular ($\theta$) samples drawn from a joint distribution obtained using a copula with quadratic sections in $v$ (Equation 12, with $a=1/\left(2\pi \right)$), a marginal gamma distribution (shape = 3, scale = 1) and a marginal von Mises distribution ($\mu =0$, $\kappa =1$). Right: PDF of the quadratic section copula with $a=1/\left(2\pi \right)$

FIGURE 4

Left column: linear (x) and circular (θ) samples drawn from joint distributions obtained with cyl_rect_combine‐copulae, a marginal gamma distribution (shape = 3, scale = 1) and a von Mises distribution ($\mu =0$, $\kappa =1$). Right column: PDFs of cyl_rect_combine‐copulae. Upper row: the rectangular patchwork of the copula consists of the two rectangles— $R_1=\left[\mathrm{0,0.5}\right]\times \left[0,1\right]$ and $R_2=\left[\mathrm{0.5,1}\right]\times \left[0,1\right]$. The function in the lower rectangle is obtained by a transformation of a Frank copula (Frank, 1979) with $\alpha =8$ and the function in the upper rectangle by transforming a 90 degrees rotated Frank copula with $\alpha =8$. Lower row: the rectangular patchwork of the copula consists of the two rectangles—R ₁ = [0.1, 0.4] × [0, 1] and $R_2=\left[\mathrm{0.6,0.9}\right]\times \left[0,1\right]$. The function in the lower rectangle is obtained by a transformation of a Frank copula ($\alpha =8$) and the function in the upper rectangle by transforming a 90 degrees rotated Frank copula with $\alpha =8$. The ‘background copula’ is a cyl_quadsec copula with parameter $a=1/\left(2\pi \right)$

FIGURE 5

Top row: 4,350 step lengths ($x$, in metres) and turn angles ($\theta$) sampled from a joint distribution obtained with the cubic sections copula cub_sec. Bottom row: 4,350 step lengths and turn angles sampled independently from their marginal distributions. Left column: scatter plots of step lengths and turn angles. Maximum likelihood estimates of the marginal densities are plotted in red and blue next to the axes. The step lengths are separated into five quantiles as marked by the colour bar below the x‐axis. Right column: circular box plots of the same data. For each of the five step length quantiles, a box plot of the corresponding angles is shown

FIGURE 6

(a) Kernel density estimate of the pseudo‐observations of the fisher data. (b) Density of the cubic sections copula cub_sec. (c) Copula density obtained from the HMM