A three component model for superdiffusive motion effectively describes migration of eukaryotic cells moving freely or under a directional stimulus

Abstract

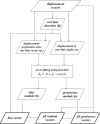
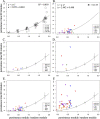
Although the simple diffusion model can effectively describe the movement of eukaryotic cells on a culture surface observed at relatively low sampling frequency, at higher sampling rates more complex models are often necessary to better fit the experimental data. Currently available models can describe motion paths by involving additional parameters, such as linearity or directional persistence in time. However sometimes difficulties arise as it is not easy to effectively evaluate persistence in presence of a directional bias. Here we present a procedure which helps solve this problem, based on a model which describes displacement as the vectorial sum of three components: diffusion, persistence and directional bias. The described model has been tested by analysing the migratory behaviour of simulated cell populations and used to analyse a collection of experimental datasets, obtained by observing cell cultures in time lapse microscopy. Overall, the method produces a good description of migration behaviour as it appears to capture the expected increase in the directional bias in presence of wound without a large concomitant increase in the persistence module, allowing it to remain as a physically meaningful quantity in the presence of a directional stimulus.

Fig 1. A three component model for single cell movement.

In the case of purely diffusive motion (A), cell displacement is modelled as a random vector of radius r. Persistent and biased movement (B and C), respectively add a persistence (p) or bias (b) vector to the random one. In the general case of combined movement (D), displacements are a combination of the three vectors and the directional component (d_b) consists of the whole bias module with the addition of random and persistence contributions (respectively r_b and p_b). The persistence contribution depends on the difference between bias and persistence angle (α angle); its length increases, according to the cosine function, when the α angles decreases.

Fig 2. Persistence and bias effect on directional component of cell movement.

The directional components of cell displacements from cell populations are plotted (y axis) against their α angles (x axis); (A, B) correspond to populations generated by simulating random (p = 0 μm; b = 0 μm), persistent (p = 8 μm; b = 0 μm), biased (p = 0 μm; b = 8 μm) and mixed movements (p = 8 μm; b = 8 μm). The continuous line corresponds to curves identified by fitting the described model to the data; the numerical parameters are shown on the top of each graph.

Fig 3. Schematic representation of the procedure for parameters evaluation.

This figure schematically reports the procedure that, starting from displacement vectors, leads to the calculation of the bias vector, the persistence module and the list of the random vectors deprived of bias and persistence components.

Fig 4. Relation between persistence evaluated as time or as vector length.

Persistence values calculated by using Formula (2) or the proposed model: results are compared by plotting, for each dataset, the resulting persistence times, normalized against the time interval (40 minutes), versus the persistence module, normalized against the corresponding random module. (A) Persistence values calculated for datasets containing 10 (circle), 20 (triangle), 30 (plus), 50 (cross) or 100 (diamond) cells simulated at different persistence levels (0, 4, 8, 12 and 16 μm) and reported in the plot as symbols of increasing sizes. For each persistence level, three replicated datasets were produced for each cell number. Fitting the indicated quadratic function to the data produced the “a” parameter value and the R² determination coefficient reported at the top. The black line represents the curve defined by the calculated “a” parameter. (B) Persistence values calculated as in (A) from NIH-3T3 (red), NIH-Ras (blue), T24 (green), HeLa (violet) and MDA-MB-231 (orange) cells moving in absence of a wound stimulus. The black line corresponds to the curve calculated by fitting the quadratic function to the experimental data as in (A). (C, D) Persistence values of unwounded (C) and wounded (D) experimental populations of Tables 1 and 3, plotted after the described normalization step and using as a reference the curve calculated in (A); the crossed bars indicate means and standard deviations of the values used to produce the curve. (E, F) The same as in (C, D) for a larger number of experimental populations.

Fig 5. Movement components of HeLa populations over time.

HeLa cell movement on a culture plate was evaluated both in absence (A-D) and in presence (E-H) of a wound stimulus. The line plots correspond to independent cell populations; for each of them, the plots report average displacements modules measured over 40 minute steps (A and E), as well as random (B and F) persistence (C and G), and bias (D and H) values, calculated from the observed displacements. Persistence and bias modules were normalized to the corresponding random module. All the values were evaluated at 40 minute intervals using the data from overlapping four hour windows.

Fig 6. Movement of different cell lines in wound healing experiments.

NIH-3T3 (orange), NIH-Ras (blue), HeLa (green), T24 (violet) and MDA-MB-231 (magenta) cell lines were grown on a culture plate and their movement was followed in both standard condition (no wound) and after stimulation (wound) by a wound inflicted to the cell layer. (A) Average distance and (B) random module, (C) persistence and (D) bias. Values reported in (C) and (D) have been normalized against the corresponding random modules. For each cell line, coloured points correspond to independent cultures analysed over a 4 hour time window, while their median value is reported as a small horizontal black trait.