Robust and Efficient Assessment of Potency (REAP) as a quantitative tool for dose-response curve estimation
- PMID: 35921131
- PMCID: PMC9348845
- DOI: 10.7554/eLife.78634
Robust and Efficient Assessment of Potency (REAP) as a quantitative tool for dose-response curve estimation
Abstract
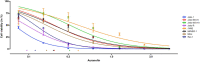
The median-effect equation has been widely used to describe the dose-response relationship and identify compounds that activate or inhibit specific disease targets in contemporary drug discovery. However, the experimental data often contain extreme responses, which may significantly impair the estimation accuracy and impede valid quantitative assessment in the standard estimation procedure. To improve the quantitative estimation of the dose-response relationship, we introduce a novel approach based on robust beta regression. Substantive simulation studies under various scenarios demonstrate solid evidence that the proposed approach consistently provides robust estimation for the median-effect equation, particularly when there are extreme outcome observations. Moreover, simulation studies illustrate that the proposed approach also provides a narrower confidence interval, suggesting a higher power in statistical testing. Finally, to efficiently and conveniently perform common lab data analyses, we develop a freely accessible web-based analytic tool to facilitate the quantitative implementation of the proposed approach for the scientific community.
Keywords: Shiny; cancer biology; dose-response; drug potency; none; quantitative tool; robust estimation; software.
Plain language summary
Finding a new drug which is both safe and efficient is an expensive and time-consuming endeavour. In particular, establishing the ‘dose-effect relationship’ – how beneficial a drug is at different dosages – can be challenging. Predicting this curve requires gathering experimental data by exposing and recording how cells respond to various levels of the drug. However, extreme values are often observed at low and high dosages, potentially introducing errors that are hard to correct in the prediction process. Yet, these extreme observations are sometimes genuine so researchers cannot just ignore them. To improve dose-effect estimation, Zhou, Liu, Fang et al. developed a new general-purpose approach. It uses advanced statistical modelling to account for extremes in lab data. This strategy outperformed other methods when dealing with these observations while also providing higher efficiency in data analysis with more uniform data in experiments. To facilitate implementation, Zhou, Liu, Fang et al. set up a user-friendly tool baptized ‘REAP’; this free online resource allows scientists without advanced statistical experience to harness the new approach and to perform dose-effect analysis more easily and accurately. This could boost research across many different disciplines that examine the effects of chemicals on cells.
© 2022, Zhou, Liu, Fang et al.
Conflict of interest statement
SZ, XL, XF, VC, MW, HW, ND, CS, JL No competing interests declared
Figures





Similar articles
-
REAP-2: An interactive quantitative tool for robust and efficient dose-response curve estimation.J Clin Transl Sci. 2023 Oct 13;7(1):e219. doi: 10.1017/cts.2023.642. eCollection 2023. J Clin Transl Sci. 2023. PMID: 38028338 Free PMC article.
-
[Standard technical specifications for methacholine chloride (Methacholine) bronchial challenge test (2023)].Zhonghua Jie He He Hu Xi Za Zhi. 2024 Feb 12;47(2):101-119. doi: 10.3760/cma.j.cn112147-20231019-00247. Zhonghua Jie He He Hu Xi Za Zhi. 2024. PMID: 38309959 Chinese.
-
Recording human electrocorticographic (ECoG) signals for neuroscientific research and real-time functional cortical mapping.J Vis Exp. 2012 Jun 26;(64):3993. doi: 10.3791/3993. J Vis Exp. 2012. PMID: 22782131 Free PMC article.
-
Dietary glycation compounds - implications for human health.Crit Rev Toxicol. 2024 Sep;54(8):485-617. doi: 10.1080/10408444.2024.2362985. Epub 2024 Aug 16. Crit Rev Toxicol. 2024. PMID: 39150724
-
Impact of summer programmes on the outcomes of disadvantaged or 'at risk' young people: A systematic review.Campbell Syst Rev. 2024 Jun 13;20(2):e1406. doi: 10.1002/cl2.1406. eCollection 2024 Jun. Campbell Syst Rev. 2024. PMID: 38873396 Free PMC article. Review.
Cited by
-
BioCurve Analyzer: a web-based shiny app for analyzing biological response curves.Plant Methods. 2025 Apr 27;21(1):55. doi: 10.1186/s13007-025-01372-x. Plant Methods. 2025. PMID: 40289147 Free PMC article.
-
REAP-2: An interactive quantitative tool for robust and efficient dose-response curve estimation.J Clin Transl Sci. 2023 Oct 13;7(1):e219. doi: 10.1017/cts.2023.642. eCollection 2023. J Clin Transl Sci. 2023. PMID: 38028338 Free PMC article.
-
Bayesian Learning of Personalized Longitudinal Biomarker Trajectory.Ann Data Sci. 2024 Jun;11(3):1031-1050. doi: 10.1007/s40745-023-00486-0. Epub 2023 Aug 1. Ann Data Sci. 2024. PMID: 38855634 Free PMC article.
References
-
- Bickel P, Doksum K. Mathematical Statistics: Basic Ideas and Selected Topics. Chapman and Hall/CRC; 2015.
-
- Blaauboer BJ, Boekelheide K, Clewell HJ, Daneshian M, Dingemans MML, Goldberg AM, Heneweer M, Jaworska J, Kramer NI, Leist M, Seibert H, Testai E, Vandebriel RJ, Yager JD, Zurlo J. The use of biomarkers of toxicity for integrating in vitro hazard estimates into risk assessment for humans. ALTEX. 2012;29:411–425. doi: 10.14573/altex.2012.4.411. - DOI - PubMed
-
- Byrne HJ, Maher MA. Numerically modelling time and dose dependent cytotoxicity. Computational Toxicology. 2019;12:100090. doi: 10.1016/j.comtox.2019.100090. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

