Disentangling personalized treatment effects from "time-of-the-day" confounding in mobile health studies

Abstract

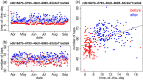
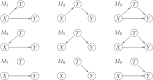
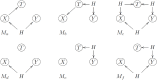
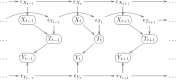
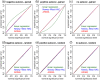
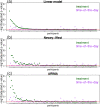
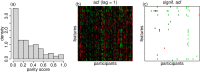
Ideally, a patient's response to medication can be monitored by measuring changes in performance of some activity. In observational studies, however, any detected association between treatment ("on-medication" vs "off-medication") and the outcome (performance in the activity) might be due to confounders. In particular, causal inferences at the personalized level are especially vulnerable to confounding effects that arise in a cyclic fashion. For quick acting medications, effects can be confounded by circadian rhythms and daily routines. Using the time-of-the-day as a surrogate for these confounders and the performance measurements as captured on a smartphone, we propose a personalized statistical approach to disentangle putative treatment and "time-of-the-day" effects, that leverages conditional independence relations spanned by causal graphical models involving the treatment, time-of-the-day, and outcome variables. Our approach is based on conditional independence tests implemented via standard and temporal linear regression models. Using synthetic data, we investigate when and how residual autocorrelation can affect the standard tests, and how time series modeling (namely, ARIMA and robust regression via HAC covariance matrix estimators) can remedy these issues. In particular, our simulations illustrate that when patients perform their activities in a paired fashion, positive autocorrelation can lead to conservative results for the standard regression approach (i.e., lead to deflated true positive detection), whereas negative autocorrelation can lead to anticonservative behavior (i.e., lead to inflated false positive detection). The adoption of time series methods, on the other hand, leads to well controlled type I error rates. We illustrate the application of our methodology with data from a Parkinson's disease mobile health study.

Fig 1. Marginal associations between treatment (before/after medication status), time-of-the-day and number of taps, for one study participant.

Panel a shows that the participant usually performs the before medication tapping tasks (red dots) earlier in the day than the after medication tasks (blue dots). Panel b shows the participant also tends to achieve better performance (larger number of taps) in tasks performed after medication. Panel c, nonetheless, also shows that large number of taps tends to be associated with later times. Hence, it is possible that the medication and/or circadian rhythms/daily routine activities might be responsible for the difference in performance between the before and after medication tapping tasks observed in this participant.

Fig 2. Putative causal models involving the X, T, and Y variables.

No causal links from Y to X or T are not allowed.

Fig 3. Alternative models involving unmeasured confounders, H.

Fig 4. Dynamic version of model M₂ in Fig 2.

Fig 5. The effect of autocorrelation on t-tests.

Here, we illustrate the effect of autocorrelation on t-tests using synthetic data simulated under the null hypothesis of no medication (or time-of-the-day effects). Panels a-c illustrate the negative autocorrelation case. Panel a shows the autocorrelation plot, of the outcome variable time series shown on panels b and c. Panel b show the time series for the outcome variable in the paired case. Panel c shows the same time-series on the random case. Red and blue dots correspond to activities performed “before” and “after” the participant has taken medication. Panels d-f illustrate the positive autocorrelation case, while panels g-i illustrate the no autocorrelation case. Panels j-l, m-o, and p-r, show the distributions of the empirical autocorrelation (lag = 1) estimates, and of t-test p-values, from 10,000 replications of the negative, positive, and no autocorrelation examples, respectively.

Fig 6. Assessing empirical type I error rates for the linear regression, Newey-West HAC, and ARIMA errors approaches.

We run 3 separate simulation experiments for the negative (panels a and d), positive (panels b and e) and no autocorrelation (panels c and f) cases. Each experiment was based on 10,000 simulated data-sets generated according to the simulation parameters presented in Table 2. All panels report the nominal significance level (α) in the x-axis, and the respective empirical type I error rate in the y-axis (computed as the proportion of p-values smaller than the nominal significance level).

Fig 7. Personalized response to putative medication and time-of-the-day effects.

Panels a, b and c show, respectively, the adjusted p-values (in -log₁₀ scale) from the union-intersection tests for putative medication effects (green dots) and putative time-of-the-day effects (purple plus signs), for the linear regression, Newey-West HAC covariance estimation, and ARIMA error models. The red horizontal lines correspond to a p-value threshold of 0.05. The order of the participants in the x-axis is the same for all panels, with the participants sorted according to the putative treatment p-value from the linear regression model (green dots) in panel a.

Fig 8. Panel a shows the distribution of the “parity score” across all participants.

The parity score was defined as the proportion of days where the participant performed the tapping task before and after taking medication on the same day. Panel b shows a heatmap of the residual autocorrelation (lag = 1) of the linear regression model fits across all feature/participant combinations. Red and green represents, respectively, negative and positive autocorrelation. Panel c shows only the autocorrelation values that were statistically different from zero according to multiple testing corrected Ljung-Box tests at a significance threshold of 0.05. (The autocorrelation values that were not statistically significant are shown in white.) Only about 4.1% of the statistically significant autocorrelations were negative.