Distribution of cholesterol in asymmetric membranes driven by composition and differential stress
- PMID: 35927954
- PMCID: PMC9674969
- DOI: 10.1016/j.bpj.2022.07.032
Distribution of cholesterol in asymmetric membranes driven by composition and differential stress
Abstract
Many lipid membranes of eukaryotic cells are asymmetric, which means the two leaflets differ in at least one physical property, such as lipid composition or lateral stress. Maintaining this asymmetry is helped by the fact that ordinary phospholipids rarely transition between leaflets, but cholesterol is an exception: its flip-flop times are in the microsecond range, so that its distribution between leaflets is determined by a chemical equilibrium. In particular, preferential partitioning can draw cholesterol into a more saturated leaflet, and phospholipid number asymmetry can force it out of a compressed leaflet. Combining highly coarse-grained membrane simulations with theoretical modeling, we investigate how these two driving forces play against each other until cholesterol's chemical potential is equilibrated. The theory includes two coupled elastic sheets and a Flory-Huggins mixing free energy with a χ parameter. We obtain a relationship between χ and the interaction strength between cholesterol and lipids in either of the two leaflets, and we find that it depends, albeit weakly, on lipid number asymmetry. The differential stress measurements under various asymmetry conditions agree with our theoretical predictions. Using the two kinds of asymmetries in combination, we find that it is possible to counteract the phospholipid number bias, and the resultant stress in the membrane, via the control of cholesterol mixing in the leaflets.
Copyright © 2022 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of interests The authors declare no competing interests.
Figures
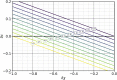
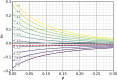

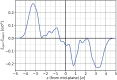

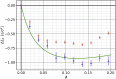
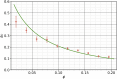
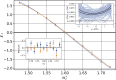
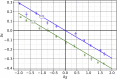
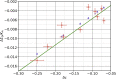
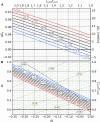
Comment in
-
Cholesterol's balancing act: Defying the status quo.Biophys J. 2022 Oct 18;121(20):3771-3773. doi: 10.1016/j.bpj.2022.08.036. Epub 2022 Aug 30. Biophys J. 2022. PMID: 36084632 Free PMC article. No abstract available.
Similar articles
-
Spontaneous Curvature, Differential Stress, and Bending Modulus of Asymmetric Lipid Membranes.Biophys J. 2020 Feb 4;118(3):624-642. doi: 10.1016/j.bpj.2019.11.3398. Epub 2019 Dec 18. Biophys J. 2020. PMID: 31954503 Free PMC article.
-
Interleaflet interaction and asymmetry in phase separated lipid bilayers: molecular dynamics simulations.J Am Chem Soc. 2011 May 4;133(17):6563-77. doi: 10.1021/ja106626r. Epub 2011 Apr 7. J Am Chem Soc. 2011. PMID: 21473645
-
Simulations of Asymmetric Membranes Illustrate Cooperative Leaflet Coupling and Lipid Adaptability.Front Cell Dev Biol. 2020 Jul 21;8:575. doi: 10.3389/fcell.2020.00575. eCollection 2020. Front Cell Dev Biol. 2020. PMID: 32850783 Free PMC article.
-
Biomembranes balance many types of leaflet asymmetries.Curr Opin Struct Biol. 2024 Aug;87:102832. doi: 10.1016/j.sbi.2024.102832. Epub 2024 May 11. Curr Opin Struct Biol. 2024. PMID: 38735128 Review.
-
Cholesterol's location in lipid bilayers.Chem Phys Lipids. 2016 Sep;199:17-25. doi: 10.1016/j.chemphyslip.2016.04.001. Epub 2016 Apr 4. Chem Phys Lipids. 2016. PMID: 27056099 Review.
Cited by
-
Membrane free-energy landscapes derived from atomistic dynamics explain nonuniversal cholesterol-induced stiffening.PNAS Nexus. 2023 Aug 17;2(8):pgad269. doi: 10.1093/pnasnexus/pgad269. eCollection 2023 Aug. PNAS Nexus. 2023. PMID: 37637198 Free PMC article.
-
Cholesterol's balancing act: Defying the status quo.Biophys J. 2022 Oct 18;121(20):3771-3773. doi: 10.1016/j.bpj.2022.08.036. Epub 2022 Aug 30. Biophys J. 2022. PMID: 36084632 Free PMC article. No abstract available.
-
Efficient Simulations of Solvent Asymmetry Across Lipid Membranes Using Flat-Bottom Restraints.J Chem Theory Comput. 2023 Sep 26;19(18):6332-6341. doi: 10.1021/acs.jctc.3c00614. Epub 2023 Aug 31. J Chem Theory Comput. 2023. PMID: 37651714 Free PMC article.
-
Combinatorial Screening of Cationic Lipidoids Reveals How Molecular Conformation Affects Membrane-Targeting Antimicrobial Activity.ACS Appl Mater Interfaces. 2023 Aug 30;15(34):40178-40190. doi: 10.1021/acsami.3c05481. Epub 2023 Aug 21. ACS Appl Mater Interfaces. 2023. PMID: 37602460 Free PMC article.
-
Induced asymmetries in membranes.Biophys J. 2023 Jun 6;122(11):2092-2098. doi: 10.1016/j.bpj.2022.12.004. Epub 2022 Dec 6. Biophys J. 2023. PMID: 36476992 Free PMC article.
References
-
- Alberts B., Johnson A., et al. Walter P. Garland Science; 2002. Molecular Biology of the Cell.
-
- Karp G. John Wiley & Sons; 2009. Cell and Molecular Biology: Concepts and Experiments.
-
- Bretscher M.S. Asymmetrical lipid bilayer structure for biological membranes. Nat. New Biol. 1972;236:11–12. - PubMed
-
- Verkleij A.J., Zwaal R.F., et al. van Deenen L.L. The asymmetric distribution of phospholipids in the human red cell membrane. A combined study using phospholipases and freeze-etch electron microscopy. Biochim. Biophys. Acta. 1973;323:178–193. - PubMed
-
- Sandra A., Pagano R.E. Phospholipid asymmetry in LM cell plasma membrane derivatives: polar head group and acyl chain distributions. Biochemistry. 1978;17:332–338. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Medical

