Inferring interiors and structural history of top-shaped asteroids from external properties of asteroid (101955) Bennu

Abstract

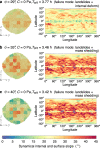
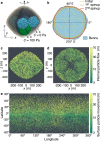
Asteroid interiors play a key role in our understanding of asteroid formation and evolution. As no direct interior probing has been done yet, characterisation of asteroids' interiors relies on interpretations of external properties. Here we show, by numerical simulations, that the top-shaped rubble-pile asteroid (101955) Bennu's geophysical response to spinup is highly sensitive to its material strength. This allows us to infer Bennu's interior properties and provide general implications for top-shaped rubble piles' structural evolution. We find that low-cohesion (≲0.78 Pa at surface and ≲1.3 Pa inside) and low-friction (friction angle ≲ 35^∘) structures with several high-cohesion internal zones can consistently account for all the known geophysical characteristics of Bennu and explain the absence of moons. Furthermore, we reveal the underlying mechanisms that lead to different failure behaviours and identify the reconfiguration pathways of top-shaped asteroids as functions of their structural properties that either facilitate or prevent the formation of moons.

Fig. 1. Surface mass movement on the Bennu-shaped rubble pile during YORP spinup.

a Cut-away schematic of the Bennu-shaped rubble-pile model, where surface particles are highlighted in beige (i.e., the top 25-m-depth layer, where the total particle number is 11,148). The blue and yellow arrows indicate the general internal deformation and surface mass movement direction. The rotation direction is indicated by the black arrows on the top. b Surface particle movement map in the case of friction angle ϕ = 29^∘, cohesion C = 0 Pa. The displacement measures the distance between a surface particle's initial position and its position at T = 4.296 h in the body-fixed frame. c, d The percentage of surface particles with displacement larger than 1 m for simulations with different friction angles and cohesive strengths, respectively. Source data are provided as a Source Data file.

Fig. 2. Pattern of internal and surface failure regions of cohesionless rubble piles.

a–c Dynamical internal slopes over a cross-section and surface slope map at the critical spin period T_crit for simulations with three friction angles ϕ, respectively. The surface regions where material can be lofted are marked with negative slopes (the bluish areas). Regional failure is initiated when the local dynamical internal/surface slope exceeds the value of ϕ, which determines the failure behaviours as indicated on the top of each panel. The dynamical internal slope are calculated based on the averaged-stress analysis using representative volume elements (the patches shown represent the elements in these cross-sections), and the dynamical surface slope are derived based on the rubble-pile alpha-shape model (Methods). Source data are provided as a Source Data file.

Fig. 3. Pattern of internal and surface failure regions of a cohesive rubble pile.

Dynamical internal pressure (a; tensile stress is expressed as a negative value) and internal and surface cohesion map (b) at the critical spin limit T_crit for a simulation with strong cohesion (C = 10 Pa). Regional failure is initiated when the local dynamical internal/surface cohesion exceeds the value of the cohesive strength C, which determines the failure behaviours as indicated on the top of this figure. The dynamical internal pressure and cohesion are calculated based on the averaged-stress analysis using representative volume elements (the patches shown represent the elements in these cross-sections), and the dynamical surface cohesion is derived based on the rubble-pile alpha-shape model (Methods). Source data are provided as a Source Data file.

Fig. 4. Bennu-shaped rubble-pile failure-mode diagram.

Failure spin periods of the four failure types as functions of the material friction (a, where C = 0 Pa) and cohesion (b, where ϕ = 29^∘) are shown by the solid curves with different colours (see Methods Section Theoretical failure conditions for the procedure to generate this diagram). The grey horizontal dashed lines with arrowheads represent some possible evolutionary pathways of rubble piles during YORP-induced spinup. Depending on the material properties, a rubble pile would end up reaching different failure curves, where its structure would fail via the corresponding failure types as indicated by the grey text. The distributions of surface slopes and cohesion of the Bennu-shaped rubble pile are shown as the median (i.e., the dashed yellow curves) and 1σ to 2σ ranges (i.e., the yellowish regions with different opacity as indicated by the double-sided arrows), indicating that only a small portion of surface area is subject to high slope/cohesion. Therefore, rubble piles can cross the Type I failure curves with local landslides, but spin periods shorter than the Types II--IV failure curves are unreachable because of global structural failure. At Bennu's current spin period (as indicated by the black vertical dashed line), surface landslides could be initiated when the material friction and cohesion are small, and its internal structure could deform if its material is cohesionless and friction angle is smaller than 22^∘. Source data are provided as a Source Data file.

Fig. 5. Reconfiguration and resurfacing of a heterogeneous top-shaped rubble pile.

a Cut-away translucent schematic of the heterogeneous model, where surface particles are highlighted in beige and internal strong cohesive spherical regions (C = 100 Pa) are highlighted in blue (whose mass centres located at the equatorial plane and radii = 80 m) and green (whose mass centre located at (x, y, z) = (0, 0, − 100) m and radius = 100 m). The friction angle ϕ = 29^∘. Two consecutive spinup-settling paths are applied to this model for testing its structural evolution (Supplementary Fig. 3). b Equatorial profile of the rubble pile at the beginning (near spherical) and the end of the two spinup-settling paths. The initial positions of the four equatorial strong regions are indicated by the yellow-dashed circles. c, d Internal particle flow of the first spinup-settling path over a centre cross-section parallel to the x–z and x–y planes, respectively. e Surface particle movement map of the first spinup-settling path. Source data are provided as a Source Data file.