Estimation and worldwide monitoring of the effective reproductive number of SARS-CoV-2
- PMID: 35938911
- PMCID: PMC9467515
- DOI: 10.7554/eLife.71345
Estimation and worldwide monitoring of the effective reproductive number of SARS-CoV-2
Abstract
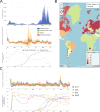
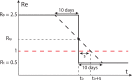
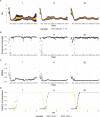
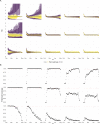
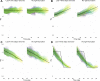
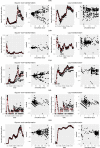
The effective reproductive number Re is a key indicator of the growth of an epidemic. Since the start of the SARS-CoV-2 pandemic, many methods and online dashboards have sprung up to monitor this number through time. However, these methods are not always thoroughly tested, correctly placed in time, or are overly confident during high incidence periods. Here, we present a method for timely estimation of Re, applied to COVID-19 epidemic data from 170 countries. We thoroughly evaluate the method on simulated data, and present an intuitive web interface for interactive data exploration. We show that, in early 2020, in the majority of countries the estimated Re dropped below 1 only after the introduction of major non-pharmaceutical interventions. For Europe the implementation of non-pharmaceutical interventions was broadly associated with reductions in the estimated Re. Globally though, relaxing non-pharmaceutical interventions had more varied effects on subsequent Re estimates. Our framework is useful to inform governments and the general public on the status of epidemics in their country, and is used as the official source of Re estimates for SARS-CoV-2 in Switzerland. It further allows detailed comparison between countries and in relation to covariates such as implemented public health policies, mobility, behaviour, or weather data.
Keywords: SARS-CoV-2; epidemiology; global health; human; infectious disease; microbiology; public health surveillance; reproductive number; viruses.
Plain language summary
Over the past two and a half years, countries around the globe have struggled to control the transmission of the SARS-CoV-2 virus within their borders. To manage the situation, it is important to have an accurate picture of how fast the virus is spreading. This can be achieved by calculating the effective reproductive number (Re), which describes how many people, on average, someone with COVID-19 is likely to infect. If the Re is greater than one, the virus is infecting increasingly more people, but if it is smaller than one, the number of cases is declining. Scientists use various strategies to estimate the Re, which each have their own strengths and weaknesses. One of the main difficulties is that infections are typically recorded only when people test positive for COVID-19, are hospitalized with the virus, or die. This means that the data provides a delayed representation of when infections are happening. Furthermore, changes in these records occur later than measures that change the infection dynamics. As a result, researchers need to take these delays into account when estimating Re. Here, Huisman, Scire et al. have developed a new method for estimating the Re based on available data records, statistically taking into account the above-mentioned delays. An online dashboard with daily updates was then created so that policy makers and the population could monitor the values over time. For over two years, Huisman, Scire et al. have been applying their tool and dashboard to COVID-19 data from 170 countries. They found that public health interventions, such as mask requirements and lockdowns, did help reduce the Re in Europe. But the effects were not uniform across the globe, likely because of variations in how restrictions were implemented and followed during the pandemic. In early 2020, the Re only dropped below one after countries put lockdowns or other severe measures in place. The Re values added to the dashboard over the last two years have been used pro-actively to inform public health policies in Switzerland and to monitor the spread of SARS-CoV-2 in South Africa. The team has also recently released programming software based on this method that can be used to track future disease outbreaks, and extended the method to estimate the Re using SARS-CoV-2 levels in wastewater.
© 2022, Huisman, Scire et al.
Conflict of interest statement
JH, JS, DA, JL, MM, SB, TS No competing interests declared, RN Reviewing editor, eLife
Figures













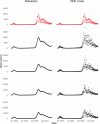

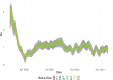
Similar articles
-
Selection for infectivity profiles in slow and fast epidemics, and the rise of SARS-CoV-2 variants.Elife. 2022 May 19;11:e75791. doi: 10.7554/eLife.75791. Elife. 2022. PMID: 35587653 Free PMC article.
-
estimateR: an R package to estimate and monitor the effective reproductive number.BMC Bioinformatics. 2023 Aug 11;24(1):310. doi: 10.1186/s12859-023-05428-4. BMC Bioinformatics. 2023. PMID: 37568078 Free PMC article.
-
Travel-related control measures to contain the COVID-19 pandemic: a rapid review.Cochrane Database Syst Rev. 2020 Oct 5;10:CD013717. doi: 10.1002/14651858.CD013717. Cochrane Database Syst Rev. 2020. Update in: Cochrane Database Syst Rev. 2021 Mar 25;3:CD013717. doi: 10.1002/14651858.CD013717.pub2. PMID: 33502002 Updated.
-
Effectiveness and cost-effectiveness of four different strategies for SARS-CoV-2 surveillance in the general population (CoV-Surv Study): a structured summary of a study protocol for a cluster-randomised, two-factorial controlled trial.Trials. 2021 Jan 8;22(1):39. doi: 10.1186/s13063-020-04982-z. Trials. 2021. PMID: 33419461 Free PMC article.
-
International travel-related control measures to contain the COVID-19 pandemic: a rapid review.Cochrane Database Syst Rev. 2021 Mar 25;3(3):CD013717. doi: 10.1002/14651858.CD013717.pub2. Cochrane Database Syst Rev. 2021. PMID: 33763851 Free PMC article.
Cited by
-
Results from Canton Grisons of Switzerland suggest repetitive testing reduces SARS-CoV-2 incidence (February-March 2021).Sci Rep. 2022 Nov 14;12(1):19538. doi: 10.1038/s41598-022-23986-0. Sci Rep. 2022. PMID: 36376420 Free PMC article.
-
Estimates of early outbreak-specific SARS-CoV-2 epidemiological parameters from genomic data.Proc Natl Acad Sci U S A. 2024 Jan 9;121(2):e2308125121. doi: 10.1073/pnas.2308125121. Epub 2024 Jan 4. Proc Natl Acad Sci U S A. 2024. PMID: 38175864 Free PMC article.
-
Practical considerations for measuring the effective reproductive number, Rt.PLoS Comput Biol. 2020 Dec 10;16(12):e1008409. doi: 10.1371/journal.pcbi.1008409. eCollection 2020 Dec. PLoS Comput Biol. 2020. PMID: 33301457 Free PMC article.
-
Evaluating the association between COVID-19 transmission and mobility in omicron outbreaks in China.Commun Med (Lond). 2025 May 20;5(1):188. doi: 10.1038/s43856-025-00906-7. Commun Med (Lond). 2025. PMID: 40394170 Free PMC article.
-
SARS-CoV-2 Genetic Diversity and Lineage Dynamics in Egypt during the First 18 Months of the Pandemic.Viruses. 2022 Aug 25;14(9):1878. doi: 10.3390/v14091878. Viruses. 2022. PMID: 36146685 Free PMC article.
References
-
- Abbott S, Hellewell J, Sherratt K, Gostic K, Hickson J, Badr HS, DeWitt M, Thompson R, Funk S. EpiNow2: estimate real-time case counts and time-varying epidemiological parameters. Zenodo. 2020a doi: 10.5281/zenodo.5036949. - DOI
-
- Abbott S, Hellewell J, Thompson RN, Sherratt K, Gibbs HP, Bosse NI, Munday JD, Meakin S, Doughty EL, Chun JY, Chan YWD, Finger F, Campbell P, Endo A, Pearson CAB, Gimma A, Russell T, Flasche S, Kucharski AJ, Eggo RM, Funk S, CMMID COVID modelling group Estimating the time-varying reproduction number of SARS-cov-2 using national and subnational case counts. Wellcome Open Research. 2020b;5:112. doi: 10.12688/wellcomeopenres.16006.2. - DOI
-
- Abbott S, Hellewell J, Thompson RN, Sherratt K, Gibbs HP, Bosse NI, Munday JD, Meakin S, Doughty EL, Chun JY, Chan YWD, Finger F, Campbell P, Endo A, Pearson CAB, Gimma A, Russell T. Temporal variation in transmission during the covid-19 outbreak. 2022. [May 10, 2022]. https://epiforecasts.io/covid/
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Research Materials
Miscellaneous

