Tunneling gravimetry

Abstract

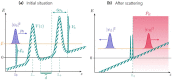
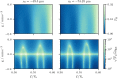
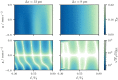
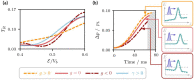
We examine the prospects of utilizing matter-wave Fabry-Pérot interferometers for enhanced inertial sensing applications. Our study explores such tunneling-based sensors for the measurement of accelerations in two configurations: (a) a transmission setup, where the initial wave packet is transmitted through the cavity and (b) an out-tunneling scheme with intra-cavity generated initial states lacking a classical counterpart. We perform numerical simulations of the complete dynamics of the quantum wave packet, investigate the tunneling through a matter-wave cavity formed by realistic optical potentials and determine the impact of interactions between atoms. As a consequence we estimate the prospective sensitivities to inertial forces for both proposed configurations and show their feasibility for serving as inertial sensors.

Keywords: Accelerometry; Fabry–Pérot interferometer; Gravimetry; Matter-wave interferometer; Quantum sensing; Quantum tunneling.

Figure 1

Gravitationally distorted matter-wave cavity and wave packet (a) prior to scattering and (b) after scattering. The matter-wave cavity consists of two Gaussian barriers with height $V_b$ and width ${\sigma }_b$, at positions $z=z_{\pm }$, chosen such that the overlap between both barriers is negligible for vanishing cavity length d. (a) The initial wave packet ${\psi }_0$ is located at $z_0$ and has an initial momentum $p_0$ that corresponds to the kinetic energy ${\mathcal{E}}_0=p_0^2/(2m)$. The gravitational field disturbs the propagation of the wave packet and the matter-wave cavity. To account for the influence of the gravitational field g, we take the kinetic energy $\mathcal{E}={\mathcal{E}}_0-mg|z_0|$ at the center of the matter-wave cavity as reference. (b) The initial wave packet scatters from the matter-wave cavity, resulting in a superposition of reflected and transmitted wave packet ${|{\psi }_L|}^2$ and ${|{\psi }_R|}^2$. To obtain the number of transmitted atoms, we introduce the operator ${\hat{P}}_R^2={\hat{P}}_R$ that projects on the region to the right of the cavity (shaded in red)

Figure 2

Transmission spectrum of a matter-wave cavity for a momentum eigenstate (solid blue) with kinetic energy $\mathcal{E}$ and for a momentum distribution (dashed blue, $\mathrm{\Delta }z=12$ μm) as well as vanishing gravitational acceleration $g=0$. The peaks in the transmission spectrum give rise to resonances whose widths increase for larger kinetic energies. We scale the distance between two resonances by the cavity length (here $d=15$ μm) and the width of the individual resonances is related to the width of the barriers (here ${\sigma }_b=1$ μm, $V_b=1.42\times {10}^{-25}\text{ J}$). The spectrum is obtained by the transfer matrix approach and discretizing the total transfer matrix into 10² sub-matrices

Figure 3

Transmission (top) of two wave packets with different initial positions $z_0$ (left and right) under the influence of gravity and the relative uncertainty (bottom) of these gravimeters. Initially, the wave packet (initial width $\mathrm{\Delta }z=12$ μm) receives the momentum kick $p_0$ and subsequently scatters from the matter-wave cavity (${\sigma }_b=1$ μm, $V_b=1.42\times {10}^{-25}\text{ J}$, and $d=15$ μm). We chose the final time of numerical evolution $t_f=1\text{ s}$ to ensure a negligible fraction of atoms remain inside the cavity. To take into account the influence of the gravitational field g prior to scattering, we take the kinetic energy $\mathcal{E}={\mathcal{E}}_0-mg|z_0|$ as reference where ${\mathcal{E}}_0=p_0^2/(2m)$ describes the initial kinetic energy and $z_0$ the initial position of the wave packet. The resonances in transmission (top) occur for the same momenta as for momentum eigenstates, but are less prominent due to the finite width Δz of the wave packet. A similar effect is induced by gravity, so that the resonances wash out for $g>0$, while they are more prominent for $g<0$. The relative uncertainty (bottom) estimates the sensitivity of the matter-wave cavity with respect to gravity by a measurement of the fraction of transmitted atoms. For small gravitational accelerations the relative uncertainty diverges. This effect is represented by white, visualizing relative uncertainties that exceed the maximum value of the colorbar. The regions of minimal uncertainty (dark blue) define the desired working points of the sensor. While $\delta g_R$ denotes the relative uncertainty for an experiment with N particles and ν repetitions, we plot the quantity $\sqrt{N}\sqrt{\nu }\delta g_R$ which is the single-particle uncertainty without repetitions, assuming shot-noise limited measurements with non-interacting particles

Figure 4

Transmission (top) of two wave packets of different initial widths Δz (left and right) under the influence of gravity and the relative uncertainty (bottom) of such a gravimeter. Initially, the wave packet receives a momentum kick $p_0$ and subsequently scatters from the matter-wave cavity (${\sigma }_b=1$ μm, $V_b=1.42\times {10}^{-25}\text{ J}$, and $d=15$ μm). We chose the final time of numerical evolution $t_f=1\text{ s}$ to ensure a negligible fraction of atoms remain inside the cavity. To take into account the influence of the gravitational field g prior to scattering, we used the kinetic energy $\mathcal{E}={\mathcal{E}}_0-mg|z_0|$ at the center of the cavity as a reference, where ${\mathcal{E}}_0=p_0^2/(2m)$ describes the initial kinetic energy and $z_0$ the initial position of the wave packet. The resonances in the transmission (top) occur for the same momenta as for momentum eigenstates, but are less prominent due to the finite width Δz of the wave packet. A similar effect is induced by gravity, so that the resonances wash out for $g>0$, while they are more prominent for $g<0$. The relative uncertainty (bottom) estimates the sensitivity of the matter-wave cavity with respect to gravity by a measurement of the fraction of transmitted atoms. Here, we omitted the term $|mg{z}_0{\partial }_{\mathcal{E}}{T}_R|$ in Eq. (5) to isolate the effect of the matter-wave cavity. For small gravitational accelerations the relative uncertainty diverges. This effect is represented by white, visualizing relative uncertainties that exceed the maximum value of the colorbar. The regions of minimal uncertainty (dark blue) define the desired working points of the sensor. While $\delta g_R$ denotes the relative uncertainty for an experiment with N particles and ν repetitions, we plot the quantity $\sqrt{N}\sqrt{\nu }\delta g_R$ which is the single-particle uncertainty without repetitions, assuming shot-noise limited measurements with non-interacting particles

Figure 5

(a) Resonances and bound states of the distorted matter-wave cavity (top) and a triangular potential (bottom). The resonances (green solid lines) of the matter-wave cavity (green) are modeled by quasi-bound states whose lifetime correspond to the width (shaded line) of the respective resonance. In contrast, the asymptotic of the triangular potential (orange) allows bound states (orange solid lines). To compare both cases, the left boundary of the triangular potential (orange) is chosen such that it correspond to the center of the left barrier of the matter-wave cavity (green). For a strong acceleration, we expect the lower resonances of the matter-wave cavity to approach the eigenenergies of the triangular potential. (b) Comparison between the transmission spectrum (red solid line) from Fig. 2 and Lorentzian profiles (blue solid lines), defined in Eq. (9), associated with the individual resonances for $g=0$. The eigenenergies and widths are obtained by a Lagrange-mesh method which diagonalizes the Hamiltonian that describes the matter-wave cavity (${\sigma }_b=1$ μm, $V_b=1.42\times {10}^{-25}\text{ J}$, and $d=15$ μm). The Lorentzian profiles show good agreement with the transmission spectrum while the overlap between resonances is negligible

Figure 6

Influence of gravity on the resonances (a) and their widths (b) of a matter wave cavity (${\sigma }_b=1$ μm, $V_b=1.42\times {10}^{-25}\text{ J}$ and $d=15$ μm). The plotted values correspond to the real and imaginary parts of the eigenvalues of the complex-scaled Hamiltonian, obtained by the Lagrange-mesh method. In addition to the resonances (solid lines), the eigenenergies of the triangular potential shown in Fig. 5(a) are included (dashed lines). If the gravitational acceleration is sufficiently strong, we expect that the right barrier becomes less important and bound states arise solely from the left barrier and the linear potential. As a consequence, the energies associated with the resonances approach the eigenenergies of the triangular potential (dashed lines). Moreover, for larger gravitational accelerations the resonances are closer to the continuum resulting in shorter lifetimes and subsequently larger widths of the resonances

Figure 7

(a) Transmission of a wave packet (initial width $\mathrm{\Delta }z=12$ μm) with initial momentum $p_0$ scattered from the matter-wave cavity (${\sigma }_b=1$ μm, $V_b=1.42\times {10}^{-25}\text{ J}$, $d=15$ μm). To take into account the influence of the gravitational field g prior to scattering, we use the kinetic energy $\mathcal{E}={\mathcal{E}}_0-mg|z_0|$ as reference where ${\mathcal{E}}_0$ describes the initial kinetic energy and $z_0$ the initial position of the wave packet. Without considering the self-interaction of the atomic cloud, the resonances wash out for $g>0$ ($g=1.3{\text{ mm/s}}^2$) and become more prominent for $g<0$ ($g=-0.8{\text{ mm/s}}^2$). A repulsive self-interaction $\gamma >0$ (here $\gamma =3.51\times {10}^{-38}\text{ m}$, $g=0{\text{ mm/s}}^2$) leads to a suppression of the resonances (dashed line). (b) Momentum width of the time-evolved wave packet. The individual plots end at the time of the turning point of a classical particle with same momentum $\mathcal{E}/V_b=0.77$. The momentum width Δp is scaled by $p_L=m{v}_R$ with the recoil velocity $v_R=5.8845\text{ mm/s}$ of the ⁸⁷Rb ${\mathrm{D}}_2$-transition. The slope of the barriers is affected by gravity and in turn deforms the wave packet upon propagation. The effect of the direction of gravity is shown in the insets to the right. As a consequence, the wave packet contracts in momentum for $g<0$, while the width is increased for $g>0$

Figure 8

(a) Gaussian wave packet ($\mathrm{\Delta }z=3$ μm) prepared in the center of the gravitationally distorted matter-wave cavity (${\sigma }_b=1$ μm, $V_b=1.42\times {10}^{-25}\text{ J}$, $d=15$ μm). A double Bragg pulse creates a superposition of the wave packet with opposite momenta $\pm p_0$. Due to gravity, the transmission of the kicked wave packet through the left (blue region) and right barrier (red region) differs. The operators ${\hat{P}}_L$ and ${\hat{P}}_R$ project on the fraction of transmitted atoms through the left (blue shaded region) and right barrier (red shaded region) where the regions either end at $z_{-}$ or start at $z_{+}$. (b) Motion of the symmetrically kicked wave packet (initial width $\mathrm{\Delta }z=3$ μm, initial kick $p_0=\pm 0.5\times \sqrt{2m{V}_b}$) prepared in the center of the matter-wave cavity for different gravitational accelerations. After a short period of time both wave packets are delocalized over the whole cavity where the white lines represent the position of the barriers. The amplitude of the resulting oscillations decreases due to periodic outcoupling of the trapped atoms

Figure 9

Asymmetric transmission (a) and relative uncertainty (b) of a wave packet starting in the center of the gravitationally distorted matter-wave cavity (${\sigma }_b=1$ μm, $V_b=1.42\times {10}^{-25}\text{ J}$, $d=15$ μm). The wave packet (initial width $\mathrm{\Delta }z=3$ μm) experiences a double Bragg pulse, resulting in a superposition of two wave packets with opposite momenta $\pm p_0$ and kinetic energies $\mathcal{E}=p_0^2/(2m)$. The asymmetric transmission corresponds to the difference between the transmission through the left and right barrier of the matter-wave cavity. (a) No resonances are observed in the asymmetric transmission because of the large initial momentum width of the (localized) wave packet. (b) The relative uncertainty associated with the asymmetric transmission contains a local maximum for small momentum kicks and shows the best sensitivity for the largest initial momentum and largest acceleration. While $\delta g_{-}$ denotes the relative uncertainty for an experiment with N particles and ν repetitions, we plot the quantity $\sqrt{N}\sqrt{\nu }\delta g_{-}$ which is the single-particle uncertainty without repetitions, assuming shot-noise limited measurements with non-interacting particles