Precision of attenuation coefficient measurements by optical coherence tomography

Abstract

Significance: Optical coherence tomography (OCT) is an interferometric imaging modality, which provides tomographic information on the microscopic scale. Furthermore, OCT signal analysis facilitates quantification of tissue optical properties (e.g., the attenuation coefficient), which provides information regarding the structure and organization of tissue. However, a rigorous and standardized measure of the precision of the OCT-derived optical properties, to date, is missing.

Aim: We present a robust theoretical framework, which provides the Cramér -Rao lower bound σμOCT for the precision of OCT-derived optical attenuation coefficients.

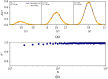
Approach: Using a maximum likelihood approach and Fisher information, we derive an analytical solution for σμOCT when the position and depth of focus are known. We validate this solution, using simulated OCT signals, for which attenuation coefficients are extracted using a least-squares fitting procedure.

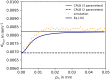
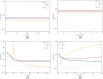
Results: Our analytical solution is in perfect agreement with simulated data without shot noise. When shot noise is present, we show that the analytical solution still holds for signal-to-noise ratios (SNRs) in the fitting window being above 20 dB. For other cases (SNR<20 dB, focus position not precisely known), we show that the numerical calculation of the precision agrees with the σμOCT derived from simulated signals.

Conclusions: Our analytical solution provides a fast, rigorous, and easy-to-use measure for OCT-derived attenuation coefficients for signals above 20 dB. The effect of uncertainties in the focal point position on the precision in the attenuation coefficient, the second assumption underlying our analytical solution, is also investigated by numerical calculation of the lower bounds. This method can be straightforwardly extended to uncertainty in other system parameters.

Keywords: Cramér–Rao lower bound; Fisher-information matrix; OCT signal simulation; attenuation coefficient; curve-fitting; maximum likelihood estimation; optical coherence tomography.

Fig. 1

Average of $N=100$ independent A-scans (blue line). The amplitudes in the underlying single A-scans follow a Rayleigh distribution and are simulated using Eq. (11) using a parameter set $\theta =[\alpha =2500,{\mu }_{\mathrm{OCT}}=2{\mathrm{mm}}^{-1},z_f=0.3\mathrm{mm},z_R=0.2\mathrm{mm},\mathrm{and}{\sigma }_{\mathrm{shot}}=7$]. The two gray dashed lines indicate the boundaries of the AFR (AFR length: $328\mu \mathrm{m}$ and sample points: $M=41$). The inset depicts the normally distributed amplitude values $S(z)$ of ${10}^4$ averaged A-scans at depth position $z=0.49\mathrm{mm}$. The amplitude at the end of the AFR is used to calculate the window-specific SNR with Eq. (13) as ${\mathrm{SNR}}_{\mathrm{AFR}}=37\mathrm{dB}$. The orange line depicts a curve fit using the square root of Eq. (4) as fit model with $\alpha$ and ${\mu }_{\mathrm{OCT}}$ free running.

Fig. 2

CRLB on the precision of ${\mu }_{\mathrm{OCT}}$ (mm⁻¹) (lines) as a function of the number of averaged A-scans $N$ in (a) the absence and (b) presence of shot noise (${\sigma }_{\mathrm{shot}}=7$). The CRLB is calculated analytically using Eq. (9) (dashed lines) and numerically based on Eq. (8) (solid lines). Model parameters $\mathbf{\theta }=[\alpha =2500,{\mu }_{\mathrm{OCT}}=[1,2,5,10]{\mathrm{mm}}^{-1},z_f=0.3\mathrm{mm},\text{\hspace{0.17em}and\hspace{0.17em}}{z}_R=0.2\mathrm{mm}]$. The dots each show the standard deviation of ${10}^4$ fitted ${\mu }_{\mathrm{OCT}}$ values using the square root of Eq. (4) as fit model, with $\alpha$ and ${\mu }_{\mathrm{OCT}}$ free running. $\mathrm{AFR}=2\mathrm{mm}$ with $M=250$ data points.

Fig. 3

CRLB on the precision of ${\mu }_{\mathrm{OCT}}$ (mm⁻¹) as a function of window-specific ${\mathrm{SNR}}_{\mathrm{AFR}}$. The black dashed line represents the CRLB in absence of noise, calculated with Eq. (9). Colored curves represent the CRLB based on Eq. (8). The dots each show the standard deviation of ${10}^4$ fitted ${\mu }_{\mathrm{OCT}}$ values. The data were simulated using $\theta =[\alpha =2500,{\mu }_{\mathrm{OCT}}=[1,2,5,10]{\mathrm{mm}}^{-1},z_f=0.3\mathrm{mm},z_R=0.2\mathrm{mm},{\sigma }_{\text{shot}}=0.1]$. Sliding $\mathrm{AFR}=328\mu \mathrm{m}$ with $M=41$ data points. $N=100$ A-scans were averaged prior to the fitting using the square root of Eq. (4) as fit model, with $\alpha$ and ${\mu }_{\mathrm{OCT}}$ free running.

Fig. 4

CRLB on the precision of ${\mu }_{\mathrm{OCT}}$ as a function of prior standard deviation of the focal point position $p_{z_f}$. The black dashed line represents the CRLB for a two-parameter model ($\alpha ,{\mu }_{\mathrm{OCT}}$), the red line represents the CRLB for a tree-parameter model ($\alpha ,{\mu }_{\mathrm{OCT}}$, $z_f$) both based on Eq. (8). The dark blue curve shows the adjusted CRLB incorporating $p_{z_f}$ using Eq. (10). The dots each show the standard deviation of ${10}^4$ fitted ${\mu }_{\mathrm{OCT}}$ values. Data are simulated using Eq. (11), $\mathbf{\theta }=[\alpha =2500,{\mu }_{\mathrm{OCT}}=2{\mathrm{mm}}^{-1},z_f=0.3\mathrm{mm},z_R=0.2\mathrm{mm},\mathrm{and}{\sigma }_{\text{shot}}=7]$; $\mathrm{AFR}=2\mathrm{mm}$ with $M=250$ data points. $N=100$ A-scans were averaged prior to the constrained fitting using the square root of Eq. (4) as fit model, with $\alpha$ and ${\mu }_{\mathrm{OCT}}$ free running and $z_f$ allowed to vary only around $z_f=0.3\mathrm{mm}\pm p_{z_f}$.

Fig. 5

$N$-times averaged Rayleigh distributed random values $⟨y⟩$ (orange dots, mean $⟨y⟩=10$) compared to a Gaussian distribution (blue line) with the same mean and variance. (a) The probability distributions of $⟨y⟩$ for $N=[\mathrm{2,30},100]$. (b) The coefficient of determination, $R^2$ between the averaged Rayleigh and normal distributions as function of $N$ (note the logarithmic horizontal scale). $R^2$ rises asymptotically towards 1, indicating that, for $N\gtrsim 30$, the averaged Rayleigh variable can be approximated as being normally distributed.

Fig. 6

Relative CRLB on the precision of $\alpha ,{\mu }_{\mathrm{OCT}}$, $z_f$, and $z_R$ (lines) as a function of the number of averaged A-scans $N$. The Cramér–Rao bounds are calculated based on Eq. (8). Model parameters $\mathbf{\theta }=[\alpha =25000,{\mu }_{\mathrm{OCT}}=0.72{\mathrm{mm}}^{-1},z_f=160\mu \mathrm{m},\text{\hspace{0.17em}and\hspace{0.17em}}{z}_R=42\mu \mathrm{m}]$. $\mathrm{AFR}=6.29\mathrm{mm}$ with $M=1000$ data points. A priori correction for noise is assumed.

Fig. 7

Relative CRLB on the precision of $\alpha ,{\mu }_{\mathrm{OCT}}$, $z_f$, and $z_R$ (lines) as a function of (a) $\alpha$, (b) ${\mu }_{\mathrm{OCT}}$, (c) $z_f$, and (d) $z_R$. Other parameters are fixed at their base values from the set $\mathbf{\theta }=[\alpha =25000,{\mu }_{\mathrm{OCT}}=0.72{\mathrm{mm}}^{-1},z_f=160\mu \mathrm{m},\text{\hspace{0.17em}and\hspace{0.17em}}{z}_R=42\mu \mathrm{m}]$. The CRLBs are calculated based on Eq. (8). $\mathrm{AFR}=6.29\mathrm{mm}$ with $M=1000$ data points. A priori correction for noise is assumed.