Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Aug 12;17(8):e0270148.
doi: 10.1371/journal.pone.0270148. eCollection 2022.

A unified fixed point approach to study the existence of solutions for a class of fractional boundary value problems arising in a chemical graph theory

Wutiphol Sintunavarat  1 , Ali Turab  1
Affiliations

A unified fixed point approach to study the existence of solutions for a class of fractional boundary value problems arising in a chemical graph theory

Wutiphol Sintunavarat et al. PLoS One. .

Abstract

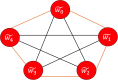
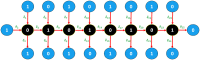
A theory of chemical graphs is a part of mathematical chemistry concerned with the effects of connectedness in chemical graphs. Several researchers have studied the solutions of fractional differential equations using the concept of star graphs. They employed star graphs because their technique requires a central node with links to adjacent vertices but no edges between nodes. The purpose of this paper is to extend the method's range by introducing the concept of an octane graph, which is an essential organic compound having the formula C8H18. In this manner, we analyze a graph with vertices annotated by 0 or 1, which is influenced by the structure of the chemical substance octane, and formulate a fractional boundary value problem on each of the graph's edges. We use the Schaefer and Krasnoselskii fixed point theorems to investigate the existence of solutions to the presented boundary value problems in the framework of the Caputo fractional derivative. Finally, two examples are provided to highlight the importance of our results in this area of study.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. A structure of a star graph G⋆ having one junction node and two edges.
Fig 2
Fig 2. An example of a non-planar graph.
Fig 3
Fig 3. Chemical bonds of an octane compound C8H18 having more than one junction nodes.
Fig 4
Fig 4. A structure of an octane compound C8H18 with labeled vertices 0 or 1.
See this image and copyright information in PMC

References

    1. Biggs NL. Algebraic Graph Theory. Cambridge: University Press; 1974.
    1. Cartwright D, Harary F. Structural balance: a generalization of Heider’s theory. Psychological Review. 1953; 63(5): 277–293. doi: 10.1037/h0046049 - DOI - PubMed
    1. Mattuck RD. A Guide to Feynman Diagrams in the Many-Body Problem. New York: McGrawHill; 1967.
    1. Avondo-Bodino G. Economic Applications of the Theory of Graphs. New York: Gordon & Breach; 1962.
    1. Harary F. Graph Theory and Theoretical Physics. New York: Academic Press; 1967. 10.1063/1.3035700 - DOI