Practical continuous-variable quantum key distribution with composable security

Abstract

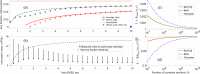
A quantum key distribution (QKD) system must fulfill the requirement of universal composability to ensure that any cryptographic application (using the QKD system) is also secure. Furthermore, the theoretical proof responsible for security analysis and key generation should cater to the number N of the distributed quantum states being finite in practice. Continuous-variable (CV) QKD based on coherent states, despite being a suitable candidate for integration in the telecom infrastructure, has so far been unable to demonstrate composability as existing proofs require a rather large N for successful key generation. Here we report a Gaussian-modulated coherent state CVQKD system that is able to overcome these challenges and can generate composable keys secure against collective attacks with N ≈ 2 × 10⁸ coherent states. With this advance, possible due to improvements to the security proof and a fast, yet low-noise and highly stable system operation, CVQKD implementations take a significant step towards their discrete-variable counterparts in practicality, performance, and security.

Fig. 1. Composability in continuous-variable quantum key distribution (CVQKD) with coherent states.

Alice and Bob obtain quantum correlations over the quantum channel by means of modulation (MOD) and local oscillator (LO) aided homodyne/heterodyne detection (HD) to prepare and measure, respectively, optical coherent states. After going through the remaining steps of the protocol that involve the authenticated channel, they obtain correlated bitstreams s_A and s_B, respectively. Certain criteria associated with correctness, robustness, and secrecy of the protocol must be satisfied, for the application to assure composable security^,. For instance, ϵ-correctness implies that Alice and Bob possess the same symmetric key s( = s_A = s_B) except with a probability ϵ_cor that bounds the probability of them having non-identical keys (Pr[s_A ≠ s_B]≤ϵ_cor). This key can be used for encrypting a message and decrypting the corresponding ciphertext across the communication channel. Dashed lines with arrows indicate classical communication across the channel and local operations. Eve is assumed to control all the channels. Further details of our CVQKD protocol implementation are presented in later sections of this article.

Fig. 2. Schematic of the experiment.

The transmitter (Tx) and receiver (Rx) were built from polarization maintaining fiber components. The transmitter comprised a 1550 nm continuous-wave laser (Tx laser), an in-phase and quadrature electro-optic modulator (IQmod) with automatic bias controller (ABC) for carrier suppression and single sideband modulation, and a variable attenuator (VATT) and Faraday isolator (FI). An arbitrary waveform generator (AWG) with 16 bit resolution and sampling rate of 1 GSps supplied waveforms RF1 and RF2 for driving IQmod. A quantum random number generator (QRNG) delivered Gaussian-distributed symbols for discrete Gaussian modulation of coherent states. The receiver comprised a laser (Rx laser; same type as Tx laser), a polarization controller (PC) to tune the incoming signal field's polarization, a symmetric beam splitter followed by a homemade balanced detector for RF heterodyning. The detector's output was sampled by a 16 bit analog-to-digital converter (ADC) at 1 GSps. BS: beam splitter, PD: photo detector. Left inset: Power spectrum of the complex waveform RF1 + ι RF2 driving the IQmod. Right inset: Power spectra of the receiver from 3 different measurements described in section “Experimental implementation”. The noise peak at 250 MHz is an interleaving spur of the ADC.

Fig. 3. Composable SKF results.

a Pseudo-temporal evolution of the composable SKF with the time parameter calculated as the ratio of the cumulative number N of complex symbols available for the classical steps of the protocol and the rate B = 100 MHz at which these symbols are modulated. b Variation of untrusted noise ξ_u measured in the experiment (lower point) and its worst-case estimator (upper point), and the noise threshold to beat to get a positive composable SKF. The deviation of the simulation traces in (a) from the experimental data between 1 and 5 s is due to the slight increase in ξ_u. c, d Comparison of confidence intervals derived in this manuscript (Beta; solid-red trace and Gaussian; dotted-green trace) with those derived in the original composable security proof (ref. ; dashed-blue trace) as a function of N. Using the confidence intervals from ref. leads to no key generation until almost the end (filled-blue square in (a) at N/B ≈ 10).