Cluster randomised trials with a binary outcome and a small number of clusters: comparison of individual and cluster level analysis method

Abstract

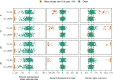
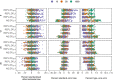
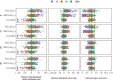
Background: Cluster randomised trials (CRTs) are often designed with a small number of clusters, but it is not clear which analysis methods are optimal when the outcome is binary. This simulation study aimed to determine (i) whether cluster-level analysis (CL), generalised linear mixed models (GLMM), and generalised estimating equations with sandwich variance (GEE) approaches maintain acceptable type-one error including the impact of non-normality of cluster effects and low prevalence, and if so (ii) which methods have the greatest power. We simulated CRTs with 8-30 clusters, altering the cluster-size, outcome prevalence, intracluster correlation coefficient, and cluster effect distribution. We analysed each dataset with weighted and unweighted CL; GLMM with adaptive quadrature and restricted pseudolikelihood; GEE with Kauermann-and-Carroll and Fay-and-Graubard sandwich variance using independent and exchangeable working correlation matrices. P-values were from a t-distribution with degrees of freedom (DoF) as clusters minus cluster-level parameters; GLMM pseudolikelihood also used Satterthwaite and Kenward-Roger DoF.

Results: Unweighted CL, GLMM pseudolikelihood, and Fay-and-Graubard GEE with independent or exchangeable working correlation matrix controlled type-one error in > 97% scenarios with clusters minus parameters DoF. Cluster-effect distribution and prevalence of outcome did not usually affect analysis method performance. GEE had the least power. With 20-30 clusters, GLMM had greater power than CL with varying cluster-size but similar power otherwise; with fewer clusters, GLMM had lower power with common cluster-size, similar power with medium variation, and greater power with large variation in cluster-size.

Conclusion: We recommend that CRTs with ≤ 30 clusters and a binary outcome use an unweighted CL or restricted pseudolikelihood GLMM both with DoF clusters minus cluster-level parameters.

Keywords: Cluster level analysis; Cluster randomised trial; Cluster-level analysis; Comparison of methods; Generalised estimating equations; Generalised linear mixed model; Small number of clusters.

Fig. 1

Performance measures of cluster-level analysis methods by number of clusters (rows), cluster size and outcome prevalence (colour). Measures shown (columns): Standardised intervention effect estimate bias, standard error bias, type-one error. Each dot represents a scenario summarised over the 1000 repetitions. All 864 scenarios are shown for each measure

Fig. 2

Performance measures of GLMM methods by number of clusters (rows), and mean cluster size (colour). Measures shown (columns): Standardised intervention effect estimate bias, standard error bias, type-one error

Fig. 3

Performance measures of GEE methods by number of clusters (rows), and mean cluster size (colour). Measures shown (columns): Standardised intervention effect estimate bias, standard error bias, type-one error

Fig. 4

Comparison of bias and type-one error of unweighted cluster-level analysis, GLMM with REPL and DF_CP, and GEE with FG standard errors and DF_CP by number of clusters (rows), and mean cluster size (colour). Measures shown (columns): Standardised intervention effect estimate bias, standard error bias, type-one error

Fig. 5

Power comparison of unweighted cluster-level analysis (CL.UNW), GLMM with REPL and DF_CP (REPL), and GEE with FG standard errors and DF_CP (FG.I) (columns) by number of clusters (rows), ICC (y axis), and variability of cluster size (colour)

Fig. 6

Motivating example results analysed by all methods considered in the simulation study. Left panel shows odds ratios and confidence intervals, right panel shows p values. Rows are analysis methods